pem (System Identification Toolbox)

Estimate the parameters of general linear models.

Syntax

m = pem(data)
m = pem(data,mi)
m = pem(data,mi,'Property1',Value1,...,'PropertyN',ValueN)
m = pem(data,orders)
m = pem(data,'nx',ssorder)
m = pem(data,'na',na,'nb',nb,'nc',nc,'nd',nd,'nf',nf,'nk',nk)
m = pem(data,orders,'Property1',Value1,...,'PropertyN',ValueN)

Description

pem is the basic estimation command in the toolbox and covers a variety of situations.

data is always an iddata object that contains the input/output data.

With Initial Model

mi is any idmodel object, idarx, idpoly, idss, or idgrey. It could be a result of another estimation routine, or constructed and modified by the constructors (idpoly, idss, idgrey) and set. The properties of mi can also be changed by any property name/property value pairs in pem as indicated in the syntax.

m is then returned as the best fitting model in the model structure defined by mi.The iterative search is initialized at the parameters of the initial/nominal model mi. m will be of the same class as mi.

Black-Box State-Space Models

With m = pem(data,n), where n is a positive integer, or m = pem(data,'nx',n) a state-space model of order n is estimated. The default situation is that it is estimated in a 'Free' parameterization, that can be further modified by the properties 'nk', 'DisturbanceModel', and 'InitialState' (see the reference pages for idss and n4sid). The model is initialized by n4sid, and then further adjusted by optimizing the prediction error fit.

You can choose between several different orders by

```
m = pem(data,'nx',[n1,n2,...nN]) 
```

and you will then be prompted for the "best" order. By

```
m = pem(data,'best')
```

an automatic choice of order among 1:10 is made.

```
m = pem(data)
```

is short for m = pem(data,'best'). To work with other delays use, e.g. m = pem(data,'best','nk',[0,...0]).

In this case m is returned as an idss model.

Black-Box Multiple-Input-Single-Output Models

The function pem also handles the general multi-input-single-output structure

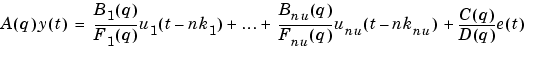
The orders of this general model are given either as

```
orders = [na nb nc nd nf nk]
```

or with (...'na',na,'nb',nb,...) as shown in the syntax. Here na, nb, nc, nd, and nf are the orders of the model and nk is the delay(s). For multi-input systems, nb, nf, and nk are row vectors giving the orders and delays of each input. (See Polynomial Representation of Transfer Functions in the "Tutorial" chapter for exact definitions of the orders.) When the orders are specified with separate entries, those not given are taken as zero.

In this case m is returned as an idpoly object.

Properties

In all cases the algorithm is affected by the properties (see Algorithm Properties for details):

Focus, with possible values 'Prediction' (Default), 'Simulation' or a SISO filter (given as an LTI or idmodel object or as filter coefficients)
MaxIter and Tolerance govern the stopping criteria for the iterative search.
LimitError deals with how the criterion can be made less sensitive to outliers and bad data
MaxSize determines the largest matrix ever formed by the algorithm. The algorithm goes into for-loops to avoid larger matrices, which may be more efficient than using virtual memory.
Trace, with possible values 'Off', 'On', 'Full', that governs the information sent to the MATLAB command window.

For black-box state-space models, also 'N4Weight' and 'N4Horizon' will affect the result, since these models are initialized with n4sid estimate. See the reference page for n4sid.

Typical idmodel properties to affect are (see idmodel properties for more details):

Ts, the sampling interval. Set 'Ts'=0 to obtain a continuous-time state-space model. For discrete-time models, 'Ts' is automatically set to sampling interval of the data. Note that, in the black box case, it is usually better to first estimate a discrete-time model, and then convert that to continuous time by d2c.
nk, the time delays from the inputs (not applicable to structured state-space models). Time delays specified by 'nk', will be included in the model.
DisturbanceModes determines the parameterization of K for free and canonical state-space parameterizations, as well as for idgrey models.
InitialState. The initial state may have a substantial influence on the estimation result for system with slow responses. It is most pronounced for Output-Error models (K=0 for state-space, and na=nc=nd=0 for input/output models). The default value 'Auto', estimates the influence of the initial state and sets the value to 'Estimate', 'Backcast' or 'Zero', based on this effect. Possible values of 'InitialState' are 'Auto', 'Estimate', 'Backcast', 'Zero' and 'Fixed'. See Initial State in the "Tutorial".

Examples

Here is an example of a system with three inputs and two outputs. A canonical form state-space model of order 5 is sought.

z = iddata([y1 y2],[ u1 u2 u3]);
m = pem(z,5,'ss','can')

Building an ARMAX model for the response to output 2.

ma = pem(z(:,2,:),'na',2,'nb',[2 3 1],'nc',2,'nk',[1 2 0])

Comparing the models (compare automatically matches the channels using the channel names).

```
compare(z,m,ma)
```

Algorithm

pem uses essentially the same algorithm as armax with modifications to the computation of prediction errors and gradients.

pe plot (iddata)