

| System Identification Toolbox |   |
Polynomial Representation of Transfer Functions
Rather than specifying the functions G and H in (3-10) in terms of functions of the frequency variable 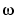 , you can describe them as rational functions of
, you can describe them as rational functions of 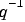 and specify the numerator and denominator coefficients in some way.
and specify the numerator and denominator coefficients in some way.
A commonly used parametric model is the ARX model that corresponds to
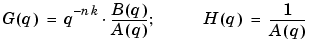
|
(3-12) |
where B and A are polynomials in the delay operator 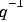 :
:
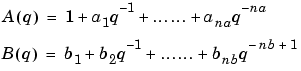
|
(3-13) |
Here, the numbers na and nb are the orders of the respective polynomials. The number nk is the number of delays from input to output. The model is usually written
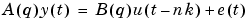
|
(3-14) |
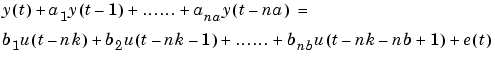
|
(3-15) |
Note that (3-14) - (3-15) apply also to the multivariable case, with ny output channels and nu input channels. Then 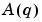 and the coefficients
and the coefficients 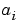 become ny-by-ny matrices,
become ny-by-ny matrices, 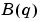 and the coefficients
and the coefficients 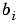 become ny-by-nu matrices.
become ny-by-nu matrices.
Another very common, and more general, model structure is the ARMAX structure
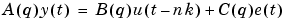
|
(3-16) |
Here, 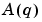 and
and 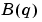 are as in (3-13), while
are as in (3-13), while
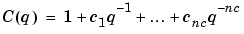
An Output-Error (OE) structure is obtained as
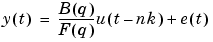
|
(3-17) |
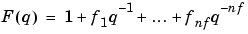
The so-called Box-Jenkins (BJ) model structure is given by
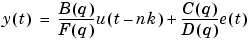
|
(3-18) |
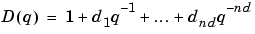
All these models are special cases of the general parametric model structure.
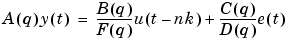
|
(3-19) |
The variance of the white noise 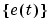 is assumed to be
is assumed to be 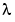 .
.
Within the structure of (3-19), virtually all of the usual linear black-box model structures are obtained as special cases. The ARX structure is obviously obtained for 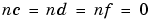 . The ARMAX structure corresponds to
. The ARMAX structure corresponds to 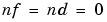 . The ARARX structure (or the "generalized least squares model") is obtained for
. The ARARX structure (or the "generalized least squares model") is obtained for 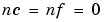 , while the ARARMAX structure (or "extended matrix model") corresponds to
, while the ARARMAX structure (or "extended matrix model") corresponds to 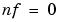 . The Output-Error model is obtained with
. The Output-Error model is obtained with 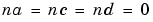 , while the Box-Jenkins model corresponds to
, while the Box-Jenkins model corresponds to 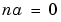 . (See Section 4.2 in Ljung (1999) for a detailed discussion.)
. (See Section 4.2 in Ljung (1999) for a detailed discussion.)
The same type of models can be defined for systems with an arbitrary number of inputs. They have the form
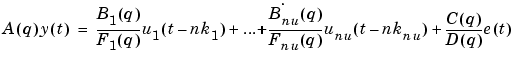
|
(3-20) |
 | The System Identification Problem | State-Space Representation of Transfer Functions |  |