System Identification Toolbox

State-Space Representation of Transfer Functions

A common way of describing linear systems is to use the state-space form.

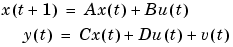
(3-21)

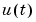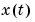Here the relationship between the input and the output is defined via the nx-dimensional state vector . In transfer function form (3-21) corresponds to (3-1) with

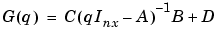
(3-22)

Here 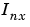is the nx by nx identity matrix. Clearly (3-21) can be viewed as one way of parametrizing the transfer function: Via (3-22) 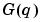becomes a function of the elements of the matrices A, B, C, and D.

To further describe the character of the noise term 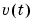in (3-21) a more flexible innovations form of the state-space model can be used.

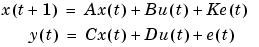
(3-23)

This is equivalent to (3-10) with 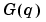given by (3-22) and 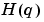by

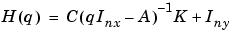
(3-24)

Here ny is the dimension of 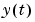and .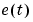

It is often possible to set up a system description directly in the innovations form (3-23). In other cases, it might be preferable to describe first the nature of disturbances that act on the system. That leads to a stochastic state-space model

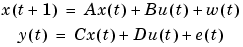
(3-25)

where and 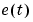are stochastic processes with certain covariance properties. In stationarity and from an input-output view, (3-25) is equivalent to (3-23) if the matrix K is chosen as the steady-state Kalman gain. How to compute K from (3-25) is described in the Control System Toolbox documentation.

Polynomial Representation of Transfer Functions

Continuous-Time State-Space Models