System Identification Toolbox

The System Identification Problem

This section discusses different basic ways to describe linear dynamic systems and also the most important methods for estimating such models.

Impulse Responses, Frequency Functions, and Spectra

The basic input-output configuration is depicted in the figure above. Assuming unit sampling interval, there is an input signal

and an output signal

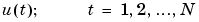
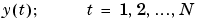
Assuming the signals are related by a linear system, the relationship can be written

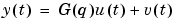
(3-1)

where q is the shift operator and 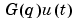is short for

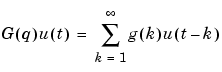
(3-2)

and

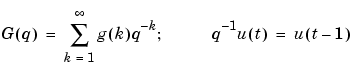
(3-3)

The numbers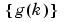are called the impulse response of the system. Clearly, 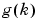is the output of the system at time k if the input is a single (im)pulse at time zero. The function 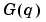is called the transfer function of the system. This function evaluated on the unit circle 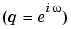gives the frequency function

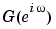
(3-4)

In (3-1) 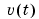is an additional, unmeasurable disturbance (noise). Its properties can be expressed in terms of its (power) spectrum

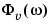
(3-5)

which is defined by

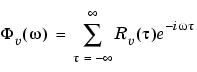
(3-6)

where 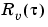is the covariance function of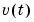

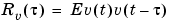
(3-7)

and E denotes mathematical expectation. Alternatively, the disturbance 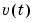can be described as filtered white noise

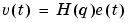
(3-8)

where 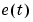is white noise with variance 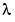and

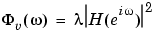
(3-9)

Equations (3-1) and (3-8) together give a time domain description of the system

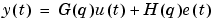
(3-10)

where G is the transfer function of the system. Equations (3-4) and (3-5) constitute a frequency domain description.

(3-11)

The impulse response (3-3) and the frequency domain description (3-11) are called nonparametric model descriptions since they are not defined in terms of a finite number of parameters. The basic description (3-10) also applies to the multivariable case; i.e., to systems with several (say nu) input signals and several (say ny) output signals. In that case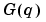is an ny-by-nu matrix while 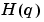and 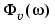are ny-by-ny matrices.

An Introductory Example to Command Mode

Polynomial Representation of Transfer Functions