System Identification Toolbox

An Introductory Example to Command Mode

A demonstration M-file called iddemo.m provides several examples of what might be typical sessions with the System Identification Toolbox. To start the demo, execute iddemo from inside MATLAB.

Before giving a formal treatment of the capabilities and possibilities of the toolbox, this example is designed to get you started with the software quickly. This example is essentially the same as demo #2 in iddemo. You may want to invoke MATLAB at this time, execute the demo, and follow along.

Data have been collected from a laboratory scale process. (Feedback's Process Trainer PT326; see page 526 in Ljung, 1999.(For references, see Reading More About System Identification in this book.) The process operates much like a common hand-held hair dryer. Air is blown through a tube after being heated at the inlet to the tube. The input to the process is the power applied to a mesh of resistor wires that constitutes the heating device. The output of the process is the air temperature at the outlet, measured in volts by a thermocouple sensor.

One thousand input-output data points were collected from the process as the input was changed in a random fashion between two levels. The sampling interval is 80 ms. The data were loaded into MATLAB in ASCII form and are now stored as the vectors y2 (output) and u2 (input) in the file dryer2.mat.

First load the data.

• load dryer2
  

It contains the input vector u2, the output vector y2. First form the data object.

• dry = iddata(y2,u2,0.08);
  

To get information about the data, just type the name.

• dry 
  

To get an overview of all the information contained in the iddata object dry, type

• get(dry)
  

For better bookkeeping, give names to input and outputs.

• dry.InputName = 'Power';
  dry.OutputName = 'Temperature';
  

Select the 300 first values for building a model.

• ze = dry(1:300); 
  

Plot the interval from sample 200 to 300.

• plot(ze(200:300)), 
  

Remove the constant levels and make the data zero-mean.

• ze = detrend(ze);
  

Let us first estimate the impulse response of the system by correlation analysis to get some idea of time constants and the like.

• impulse(ze,'sd',3) 
  

This gives a plot with dash-dotted lines marking a confidence region corresponding to three standard deviations (ca 99.9%). From this it is easy to see if there is a time delay in the system.

The simplest way to get started, is to build a state-space model where the order is automatically determined, using a prediction error method.

• m1 = pem(ze)
  

When the calculations are finished, a display of the basic information about m1 is shown. Anytime m1 is typed, this display is shown. Typing present(m1) will give some more information about the model, including uncertainties.

To retrieve the properties of this model we could, e.g., find the A matrix of the state space representation by

• A = m1.a
  

m1 is a model object, and

• get(m1)
  

gives a list of all information stored in the model.

How good is this model? One way to find out is to simulate it and compare the model output with measured output. We then select a portion of the original data that was not used to build the model, e.g., from sample 800 to 900.

• zv = dry(800:900);
  zv = detrend(zv);
  compare(zv,m1); 
  

The Bode plot of the model is obtained by

• bode(m1) 
  

An alternative is to consider the Nyquist plot, and mark uncertainty regions at certain frequencies with ellipses, corresponding to 3 (say) standard deviations:

• nyquist(m1,'sd',3) 
  

We can also compare the step response of the model with one that is directly computed from data (ze) in a nonparametric way.

• step(m1,ze) 
  

To study a model with prescribed structure, we compute a difference equation model with two poles, one zero, and three delays.

• m2 = arx(ze,[2 2 3])
  

This gives a model of the form

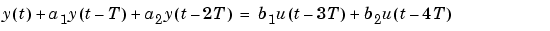
where T is the sampling interval (here 0.08 seconds). This model, known as an ARX model, tries to explain or compute the value of the output at time t, given previous values of y and u. To compare its performance on validation data with m1, type

• compare(zv,m1,m2); 
  

Compute and plot the poles and zeros of the models.

• pzmap(m1,m2) 
  

The uncertainties of the poles and zeros can also be plotted.

• pzmap(m1,m2,'sd',3), % '3' denotes the number of standard 
  deviations
  

Estimate the frequency response by a nonparametric spectral analysis method.

• gs = spa(ze);
  

Compare with the frequency functions from the parametric models.

• bode(m1,m2,gs) 
  

The Toolbox Commands

The System Identification Problem