

| System Identification Toolbox |   |
Continuous-Time State-Space Models
It is often easier to describe a system from physical modeling in terms of a continuous-time model. The reason is that most physical laws are expressed in continuous time as differential equations. Therefore, physical modeling typically leads to state-space descriptions like
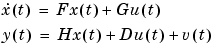
|
(3-26) |
Here, 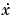 means the time derivative of
means the time derivative of 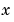 . If the input is piece-wise constant over time intervals
. If the input is piece-wise constant over time intervals 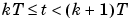 , then the relationship between
, then the relationship between 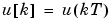 and
and 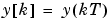 can be exactly expressed by (3-21) by taking
can be exactly expressed by (3-21) by taking
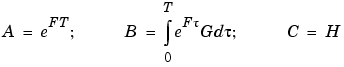
|
(3-27) |
and associate 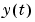 with
with 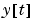 , etc. If you start with a continuous-time innovations form
, etc. If you start with a continuous-time innovations form
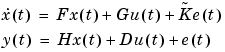
|
(3-28) |
the discrete-time counterpart is given by (3-23) where still the relationships (3-27) hold. The exact connection between 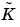 and
and 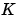 is somewhat more complicated, though. An ad hoc solution is to use
is somewhat more complicated, though. An ad hoc solution is to use
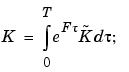
|
(3-29) |
in analogy with G and B. This is a good approximation for short sampling intervals T.
 | State-Space Representation of Transfer Functions | Estimating Impulse Responses |  |