System Identification Toolbox

Estimating Impulse Responses

Consider the descriptions (3-1) and (3-2). To directly estimated the impulse response coefficients, also in the multivariable case, it is suitable to define a high order Finite Impulse Response (FIR) model.

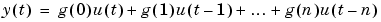
(3-30)

and estimate the g-coefficients by the linear least squares method. In fact, to check if there are non-causal effects from input to output, e.g., due to feedback from y in the generation of u (closed loop data), g for negative lags can also be estimated.

(3-31)

If u is white noise, the impulse response coefficients will be correctly estimated, even if the true dynamics from u to y is more complicated than these models. Therefore it is natural to filter both the output and the input through a filter that makes the input sequence as white as possible, before estimating the g. This is the essence of correlation analysis for estimating impulse responses.

Continuous-Time State-Space Models

Estimating Spectra and Frequency Functions