System Identification Toolbox

idpoly

Construct an idpoly model for input-output models.

Syntax

• m = idpoly(A,B)
  m = idpoly(A,B,C,D,F,NoiseVariance,Ts)
  m = idpoly(A,B,C,D,F,NoiseVariance,Ts,'Property1',Value1,...
          'PropertyN',ValueN)
  

m = idpoly(mi)

Description

idpoly creates a model object containing parameters that describe the general multi-input-single-output model structure.

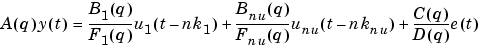
A, B, C, D, and F specify the polynomial coefficients.

For single-input systems, these are all row vectors in the standard MATLAB format.

• A = [1 a1 a2 ...  ana]
  

consequently describes

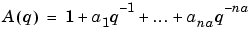
A, C, D, and F all start with 1, while B contains leading zeros to indicate the delays. See "Polynomial Representation of Transfer Functions in the "Tutorial" chapter.

For multi-input systems, B and F are matrices with one row for each input.

For time series, B and F are entered as empty matrices.

• B = [];   F = [];
  

NoiseVariance is the variance of the white noise sequence 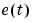, while Ts is the sampling interval.

Trailing arguments C, D, F, NoiseVariance, and Ts can be omitted, in which case they are taken as 1. (If B=[], then F is taken as [].) The property name/property value pairs can start directly after B.

Ts = 0 means that the model is a continuous-time one. Then the interpretation of the arguments is that

• A = [1 2 3 4]
  

corresponds to the polynomial 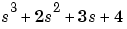in the Laplace variable s, and so on. For continuous-time systems NoiseVariance indicates the level of the spectral density of the innovations. A sampled version of the model has the innovations variance NoiseVariance/Ts, where Ts is the sampling interval. The continuous-time model must have a white noise component in its disturbance description. See the section Spectrum Normalization and the Sampling Interval in the "Tutorial".

For discrete-time models (Ts>0), note the following: idpoly strips any trailing zeros from the polynomials when determining the orders. It also strips leading zeros from the B polynomial to determine the delays. Keep this in mind when you use idpoly and polydata to modify earlier estimates to serve as initial conditions for estimating new structures. See the section Initial Parameter Values in the "Tutorial".

idpoly can also take any single-output idmodel or LTI-object mi as input argument. If an LTI-system has an input group with name `Noise', these inputs will be interpreted as white noise with unit variance, and the noise model of the idpoly model will be computed accordingly.

Properties

The properties of the idpoly object can be summarized as follows:

• na, nb, nc, nd, nf, nk: The orders and delays of the polynomials. Integers or row vectors of integers.
• a, b, c, d, f: The polynomials, described by row vectors and matrices as detailed above.
• da, db, dc, dd, df: The estimated standard deviation of the polynomials. Cannot be set.
• InitialState: How to deal with the initial conditions that are required to compute the prediction of the output: Possible values
• 'Estimate': The necessary initial states are estimated from data as extra parameters
• 'Backcast': The necessary initial states are estimated by a backcasting (backwards filtering) process, described in Knudsen (1994)
• 'Zero': all initial states are taken as zero
• 'Auto': An automatic choice between the above is made, guided by the data.

In addition, any idpoly object also has all the properties of idmodel. See idmodel properties and Algorithm Properties.

Note that all properties can be set or retrieved either by set/get or by subscripts. Autofill applies to all properties and values, and are these case insensitive.

• m.a=[1 -1.5 0.7];
  set(m,'ini','b')
  p = roots(m.a)
  

For a complete list of property values, use get(m). To see possible value assignments, use set(m). See also idprops idpoly.

Examples

To create a system of ARMAX, type

• A = [1 -1.5 0.7];
  B = [0 1 0.5];
  C = [1 -1 0.2];
  m0 = idpoly(A,B,C);
  

This gives a system with one delay (nk = 1).

Create the continuous-time model

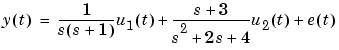
Sample it with T=0.1 and then simulate it without noise.

• B=[0 1;1 3];
  F=[1 1 0;1 2 4]
  m = idpoly(1,B,1,1,F,1,0)
  md = c2d(m,0.1)
  y = sim(md,[u1 u2]);
  

Note that the continuous time model will automatically be sampled to the sampling interval of the data, when simulated, so the above is also achieved by

• u = iddata([],[u1 u2],0.1)
  y = sim(m,u)
  

See Also

sim, idss

References

See Ljung (1999) Section 4.2 for the model structure family.

See

T. Knudsen (1994): A new method for estimating ARMAX models. In Proc. 10th IFAC Symposium on System Identification, pp 611-617. Copenhagen, Denmark

for the backcast method.

idmodred

idss