System Identification Toolbox

Spectrum Normalization and the Sampling Interval

In the function spa the spectrum estimate is normalized with the sampling interval T as

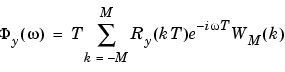
(3-67)

where

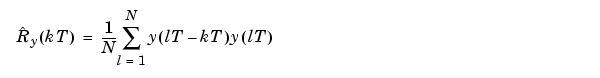
(See also (3-3)). The normalization in etfe is consistent with (3-67). This normalization means that the unit of 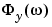is "power per radians/time unit" and that the frequency scale is "radians/time unit." You then have

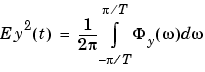
(3-68)

In MATLAB, therefore, you hav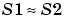e where

• y.ts = T
  sp = spa(y); 
  phiy = squeeze(sp.spec) % squeeze takes out the spurios dimensions
  S1 = sum(phiy)/length(phiy)/T;
  S2 = sum(y.^2)/size(y,1);
  

Note that PHIY contains 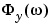between 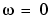and 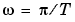with a frequency step of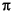 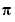/ (T length(phiy)). The sum S1 is, therefore, the rectangular approximation of the integral in (3-68). The spectrum normalization differs from the one used by spectrum in the Signal Processing Toolbox, and the above example shows the nature of the difference.

The normalization with T in (3-67) also gives consistent results when time series are decimated. If the energy above the Nyquist frequency is removed before decimation (as is done in resample), the spectral estimates coincide; otherwise you see folding effects.

Try the following sequence of commands.

• m0 = idpoly(1,[ ],[1 1 1 1]);
         % 4th order MA-process
  e = idinput(2000,'rgs')
  e = iddata([], e, 'Ts', 1);
  y = sim(m0, e);
  g1 = spa(y);
  g2 = spa(y(1:4:2000)); % This code automatically sets Ts to 4.
  ffplot(g1,g2) % Folding effects
  g3 = spa(resample(y,1,4)); % Prefilter applied
  ffplot(g1,g3) % No folding
  

For a parametric noise (time series) model

the spectrum is computed as

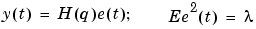
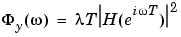
(3-69)

which is consistent with (3-67) and (3-68). Think of 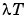as the spectral density of the white noise source .

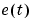When a parametric disturbance model is transformed between continuous time and discrete time and/or resampled at another sampling rate, the functions c2d and d2c in the System Identification Toolbox use formulas that are formally correct only for piecewise constant inputs. (See (3-29)). This approximation is good when T is small compared to the bandwidth of the noise. During these transformations the variance 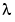of the innovations 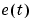is changed so that the spectral density T . 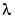remains constant. This has two effects:

• The spectrum scalings are consistent, so that the noise spectrum is essentially invariant (up to the Nyquist frequency) with respect to resampling.
• Simulations with noise using sim has a higher noise level when performed at faster sampling.

This latter effect is well in line with the standard description that the underlying continuous-time model is subject to continuous-time white noise disturbances (which have infinite, instantaneous variance), and appropriate low-pass filtering is applied before sampling the measurements. If this effect is unwanted in a particular application, scale the noise source appropriately before applying sim.

Note the following cautions relating to these transformations of disturbance models. Continuous-time disturbance models must have a white noise component. Otherwise the underlying state-space model, which is formed and used in c2d and d2c, is ill-defined. Warnings about this are issued by idpoly and these functions. Modify the C-polynomial accordingly. Make the degree of the monic C-polynomial in continuous time equal to the sum of the degrees of the monic A- and D-polynomials; i.e., in continuous time.

• length(C)-1 = (length(A)-1)+(length(D)-1)
  

Linear Regression Models

Interpretation of the Loss Function