System Identification Toolbox

Algorithm Properties

Describe the algorithm properties that affect the estimation process.

Syntax

• idprops algorithm
  m.algorithm
  

Description

All the idmodel objects in the toolbox, idarx, idss, idpoly, and idgrey, have a property Algorithm, which is a structure that contains a number of options that govern the estimation algorithms. The fields of this structure can be individually set and retrieved in the usual way, such as get(m,'MaxIter') or m.SearchDirection = 'gn'. Also, autofill applies and the names are case insensitive.

Note    Algorithm is a property of idmodel. Any algorithm property can be separately set as above. Also, if you have a standard algorithm setup that you prefer, you can set those properties simultaneously as in m = pem(Data,mi,'alg',myalg).

Note    The algorithm properties, like all other model properties, will be inherited by the resulting model m. If you continue the estimation using m as initial model, all previously set algorithm features will thus apply, unless you specify otherwise.

The fields of Algorithm are as follows:

Applying to all estimation methods

• Focus: This property affects the weighting applied to the fit between the model and the data. It can be used to assure that the model approximates the true system well over certain frequency intervals. Focus can assume the following values:
• 'Prediction': This is the default and means that the model is determined by minimizing the prediction errors. It corresponds to a frequency weighting that is given by the input spectrum times the inverse noise model. Typically, this favors a good fit at high frequencies. From a statistical variance point of view, this is the optimal weighting, but then the approximation aspects (bias) of the fit are neglected.
• 'Simulation': This means that frequency weighting of the transfer function fit is given by the input spectrum. Frequency ranges where the input has considerable power will thus be better described by the model. In other words, the model approximation is such that the model will produce as good simulations as possible, when applied to inputs with the same spectra as used for the estimation. For models that have no disturbance model, that is y = G u + e, (A=C=D=1 for idpoly models and K=0 for idss models) there is no difference between 'Simulation' and 'Prediction'. For models with a disturbance description, i.e. y = Gu + H e, G is first estimated with H = 1 and then H is estimated by a prediction error method, keeping the estimated transfer function 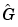fixed. This option will also guarantee a stable transfer function G.
• 'Stability': The resulting model is guaranteed to be stable, but a prediction weighing is still maintained. Note that forcing the model to be stable could mean that a bad model is obtained. Use only when you know the system to be stable.
• Any SISO linear filter. Then the transfer function from input to output is determined by a frequency fit with this filter times the input spectrum as weighting function. The disturbance model is determined by a prediction error method, keeping the transfer function estimate fixed, as in the simulation case. To obtain a good model fit over a special frequency range, the filter should thus be chosen with a passband over this range. For a model with no disturbance model, the result is the same as first applying prefiltering to data using idfilt. The filter can be specified in a few different ways as:
• Any single-input-single-output idmodel
• An ss, tf or zpk model from the Control System Toolbox
• {A,B,C,D} with the state-space matrices for the filter
• {numerator, denominator} with the transfer function numerator/denominator of the filter
• MaxSize: No matrix with more than MaxSize elements is formed by the algorithm. Instead, for-loops will be used. MaxSize will thus decide the memory/speed trade-off, and can prevent slow use of virtual memory. MaxSize can be any positive integer, but it is required that the input-output data contain less than MaxSize elements. The default value of MaxSize is 'Auto', which means that the value is determined in the M-file idmsize. You can edit this file to optimize speed on a particular computer.
• FixedParameter: A list of parameters that will be kept fixed to the nominal/initial values and not estimated. This is a vector of integers containing the indices of the fixed parameters. The numbering of the parameters is the same as in the model property 'ParameterVector'. The parameter names from the property 'PName' can also be used. For structured state-space models, it is easier to fix/unfix parameters by the structure matrices, As, Bs, etc. See idss. When using parameter names to specify the fixed parameters, Fixedparameter is a cell array of strings. The strings may contain the wildcards `*' (meaning any continuation of the given string) and `?' (meaning any character). For example, if all disturbance model parameters start with `k', FixedParameter = {'k*'} will fix all these parameters. The function setpname may be useful in this context.

Applying to n4sid, estimating state-space models

These also apply to pem for estimating black-box state-space models, since these are initialized by the n4sid estimate.

• N4Weight: This property determines some weighting matrices used in the singular-value decomposition that is a central step in the algorithm. Two choices are offered: 'MOESP', which corresponds to the MOESP algorithm by Verhaegen, and 'CVA', which is the canonical variable algorithm by Larimore. See the reference page for n4sid. The default value is 'N4Weight' = 'Auto', which gives an automatic choice between the two options.
• N4Horison: Determines the prediction horizons forward and backward, used by the algorithm. This is a row vector with three elements:
  N4Horison =[r sy su], where r is the maximum forward prediction horizon, i.e., the algorithms uses up to r-step ahead predictors. sy is the number of past outputs, and su is the number of past inputs that are used for the predictions. For an exact definition of these integers, see pages 209-210 in Ljung(1999), where they are called r, s1 and s2. These numbers may have a substantial influence of the quality of the resulting model, and there are no simple rules for choosing them. Making 'N4Horizon' a k-by-3 matrix means that each row of 'N4Horison' will be tried out, and the value that gives the best (prediction) fit to data will be selected. (This option cannot be combined with selection of model order.) If you specify only one column in 'N4Horizon', the interpretation is r=sy=su. The default choice is 'N4Horizon' = 'Auto', which uses an Akaike Information Criterion (AIC) for the selection of sy and su.

Applying to estimation methods using iterative search for minimizing a criterion, i.e., armax, bj, oe, and pem

• Trace: This property determines the information about the iterative search that is provided to the MATLAB command window.
• 'Trace' = 'Off': No information is written to the screen.
• 'Trace' = 'On': Information about criterion values and the search process is given for each iteration.
• 'Trace'= 'Full': The current parameter values and the search direction are also given (except in the 'Free' SSParameterization case for idss models)
• LimitError: This variable determines how the criterion is modified from quadratic to one that gives linear weight to large errors. Errors larger than LimitError times the estimated standard deviation will carry a linear weight in the criterions.The default value of LimitError is 1.6. LimitError = 0 disables the robustification and leads to a purely quadratic criterion. The standard deviation is estimated robustly as the median of the absolute deviations from the median, divided by 0.7. (See Eq. (15.9)-(15.10) in Ljung (1999)).
• MaxIter: The maximum number of iterations performed during the search for minimum. The iterations will stop when MaxIter is reached, or some other stopping criterion is satisfied. The default value of MaxIter is 20. Setting MaxIter = 0 will return the result of the start-up procedure. The actual number of used iterations is given by the property EstimationInfo.Iterations.
• Tolerance: Based on the Gauss-Newton vector computed at the current parameter value, an estimate is made of the expected improvement of the criterion at the next iteration. When this expected improvement is less than Tolerance, measured in percent, the iterations are stopped. Default value: 0.01.
• SearchDirection: The direction along which a line search is performed to find a lower value of the criterion function. It may assume the following values:
• 'gn': The Gauss-Newton direction (inverse of the Hessian times the gradient direction). If no improvement is found along this direction, the gradient direction is also tried out.
• 'gns': A regularized version of the Gauss-Newton direction. Eigenvalues less than GnsPinvTol (see "Advanced" below) of the Hessian are neglected, and the Gauss-Newton direction is computed in the remaining subspace.
• 'lm': The Levenberg-Marquard method is used. This means that the next parameter value is -pinv(H+d*I)*grad from the previous one, where H is the Hessian, I is the identity matrix, grad is the gradient. d is a number that is increased until a lower value of the criterion is found.
• 'Auto': A choice between the above is made in the algorithm. This is the default choice.
• Advanced: This is a structure that contains detailed algorithm choices, that normally the user does not need to get involved in. For detailed explanations, the code will have to be examined. 'Advanced' has the following fields:
• Search: Contains fields with relevance for the iterative search:
1. GnsPinvTol: The tolerance for the pseudoinverse used to compute the gns direction. See above. Default 10^-9.
2. LmStep: The next value of d in the LM method is lmstep times the previous one. Default lmstep = 2.
3. StepReduction: In the line search used for other directions than LM, the step is reduced by the factor stepred in each try. Default: StepReduction = 2.
4. MaxBisection: The maximum number of bisections used by the line search along the search direction. Default 10.
5. LmStartValue: The starting value of d in the LM method. Default 0.001.
6. RelImprovement: The iterations are stopped if the relative improvement of the criterion is less than relimp. Default RelImprovement= 0.
• Threshold: Contains fields with thresholds for several tests:
1. Sstability: used for stability test of continuous time models. Model is considered stable if its rightmost pole is to the left of Sstability. Default 0.
2. Zstability: used for stability test of discrete time models. Model is considered stable if all poles are within the distance Zstability from the origin. Default 1.01.
• AutoInitialState: When InitialState = 'Auto', the state will be estimated if the ratio of the prediction error norm with zero initial state, to the norm with estimated initial state exceeds AutoInitialState. Default 1.2.

See Also

armax, bj, EstimationInfo, n4sid, oe, pem

Reference

For the iterative minimization, see Dennis, J.E. Jr. and R.B. Schnabel. Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice Hall, Englewood Cliffs, N.J. 1983.

For a general reference to the identification algorithms, see Ljung (1999), Chapter 10.

aic

ar