bj (System Identification Toolbox)

Estimate the parameters of a Box-Jenkins model.

Syntax

m = bj(data,orders)
m = bj(data,'nb',nb,'nc',nc,'nd',nd,'nf',nf,'nk',nk)
m = bj(data,orders,'Property1',Value1,'Property2',Value2,...)

Description

bj returns m as an idpoly object with the resulting parameter estimates, together with estimated covariances. The bj function estimates parameters of the Box-Jenkins model structure

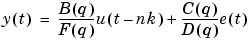
using a prediction error method.

data is an iddata object containing the output-input data. The model orders can be specified by setting the argument orders to

```
orders = [ nb nc nd nf nk]
```

The parameters nb, nc, nd, and nf are the orders of the Box-Jenkins model and nk is the delay. Specifically,

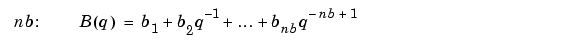
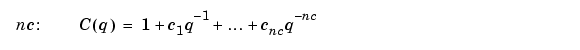
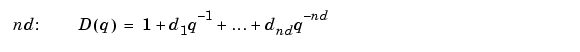
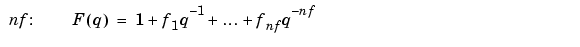
The orders can also be defined as property name/property value pairs (...,'nb',nb,...). Alternatively, you can specify the vector as

```
orders = mi
```

where mi is an initial guess at the Box-Jenkins model given in idpoly format. See Polynomial Representation of Transfer Functions in the "Tutorial" for more information.

For multi-input systems, nb, nf, and nk are row vectors with as many entries as there are input channels. Entry number i then describes the orders and delays associated with the i-th input.

The structure and the estimation algorithm are affected by any property name/property value pairs that are set in the input argument list. Useful properties are 'Focus', 'InitialState', 'Trace', 'MaxIter', 'Tolerance', 'LimitError', and 'FixedParameter'.

See Algorithm Properties and the reference pages for idmodel and idpoly for details of these properties and their possible values.

bj does not support multi-output models. Use state-space model for this case (see n4sid and pem).

Examples

Here is an example that generates data and stores the results of the startup procedure separately.

B = [0 1 0.5];
C = [1 -1 0.2];
D = [1 1.5 0.7];
F = [1 -1.5 0.7];
m0 = idpoly(1,B,C,D,F,0.1);
e = iddata([],randn(200,1));
u = iddata([],idinput(200)); 
y = sim(m0,[u e]);
z = [y u];
mi = bj(z,[2 2 2 2 1],'MaxIter',0)
m = bj(z,mi)
m.EstimationInfo
m = bj(z,m); % Continue if m.es.WhyStop shows that maxiter has 
             % been reached.
compare(z,m,mi)

Algorithm

bj uses essentially the same algorithm as armax with modifications to the computation of prediction errors and gradients.

arxstruc bode