oe (System Identification Toolbox)

Estimate the parameters of an Output-Error model.

Syntax

m = oe(data,orders)
m = oe(data,'nb',nb,'nf',nf,'nk',nk)
m = oe(data,orders,'Property1',Value1,'Property2',Value2,...)

Description

oe returns m as an idpoly object with the resulting parameter estimates, together with estimated covariances.The parameters of the Output-Error model structure

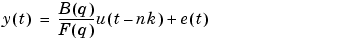
are estimated using a prediction error method.

data is an iddata object containing the output-input data. The structure information can either be given explicitly as (...,'nb',nb,'nf',nf,'nk',nk,...), or in the argument orders given as

```
orders = [nb nf nk]
```

The parameters nb and nf are the orders of the Output-Error model and nk is the delay. Specifically,

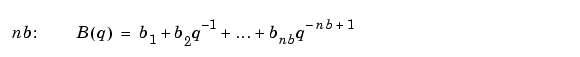
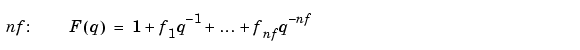
Alternatively, you can specify the vector as

```
orders = mi
```

where mi is an initial guess at the Output-Error model given in idpoly format. See Polynomial Representation of Transfer Functions in the "Tutorial" chapter for more information.

For multi-input systems, nb, nf, and nk are row vectors with as many entries as there are input channels. Entry number i then describes the orders and delays associated with the i-th input.

The structure and the estimation algorithm are affected by any property name/property value pairs that are set in the input argument list. Useful properties are 'Focus', 'InitialState', 'InputDelay', 'SearchDirection', 'MaxIter', 'Tolerance', 'LimitError', 'FixedParameter', and 'Trace'.

See Algorithm Properties, idpoly, and idmodel for details of these properties and their possible values.

oe does not support multi-output models. Use state-space model for this case (see n4sid and pem).

Algorithm

oe uses essentially the same algorithm as armax with modifications to the computation of prediction errors and gradients.

See Also

armax, bj, idpoly, pem

n4sid pe