Optimization Toolbox

Multiobjective Examples

The previous examples involved problems with a single objective function. This section demonstrates solving problems with multiobjective functions using lsqnonlin, fminimax, and fgoalattain. Included is an example of how to optimize parameters in a Simulink model.

Simulink Example

Let's say that you want to optimize the control parameters in the Simulink model optsim.mdl. (This model can be found in the Optimization Toolbox optim directory. Note that Simulink must be installed on your system to load this model.) The model includes a nonlinear process plant modeled as a Simulink block diagram shown in Figure 2-1, Plant with Actuator Saturation.

Figure 2-1: Plant with Actuator Saturation

The plant is an under-damped third-order model with actuator limits. The actuator limits are a saturation limit and a slew rate limit. The actuator saturation limit cuts off input values greater than 2 units or less than -2 units. The slew rate limit of the actuator is 0.8 units/sec. The open-loop response of the system to a step input is shown in Figure 2-2, Closed-Loop Response. You can see this response by opening the model (type optsim at the command line or click the model name), and selecting Start from the Simulation menu. The response plots to the scope.

Figure 2-2: Closed-Loop Response

The problem is to design a feedback control loop that tracks a unit step input to the system. The closed-loop plant is entered in terms of the blocks where the plant and actuator have been placed in a hierarchical Subsystem block. A Scope block displays output trajectories during the design process. See Figure 2-3, Closed-Loop Model.

Figure 2-3: Closed-Loop Model

One way to solve this problem is to minimize the error between the output and the input signal. The variables are the parameters of the PID controller. If you only need to minimize the error at one time unit, it would be a single objective function. But the goal is to minimize the error for all time steps from 0 to 100, thus producing a multiobjective function (one function for each time step).

The routine lsqnonlin is used to perform a least-squares fit on the tracking of the output. This is defined via a MATLAB function in the file tracklsq.m, shown below, that defines the error signal. The error signal is yout, the output computed by calling sim, minus the input signal 1.

The function tracklsq must run the simulation. The simulation can be run either in the base workspace or the current workspace, i.e., the workspace of the function calling sim, which in this case is tracklsq's workspace. In this example, the simset command is used to tell sim to run the simulation in the current workspace by setting 'SrcWorkspace' to 'Current'.

To run the simulation in optsim, the variables Kp, Ki, Kd, a1, and a2 (a1 and a2 are variables in the Plant block) must all be defined. Kp, Ki, and Kd are the variables to be optimized. You can initialize a1 and a2 before calling lsqnonlin and then pass these two variables as additional arguments. lsqnonlin then passes a1 and a2 to tracklsq each time it is called, so you do not have to use global variables.

After choosing a solver using the simset function, the simulation is run using sim. The simulation is performed using a fixed-step fifth-order method to 100 seconds. When the simulation completes, the variables tout, xout, and yout are now in the current workspace (that is, the workspace of tracklsq). The Outport block is used in the block diagram model to put yout into the current workspace at the end of the simulation.

Step 1: Write an M-file tracklsq.m.

• function F = tracklsq(pid,a1,a2)
  Kp = pid(1);       % Move variables into model parameter names
  Ki = pid(2);
  Kd = pid(3);
  % Choose solver and set model workspace to this function
  opt = simset('solver','ode5','SrcWorkspace','Current');
  [tout,xout,yout] = sim('optsim',[0 100],opt);
  F = yout-1;        % Compute error signal
  

Step 2: Invoke optimization routine.

• optsim                      % Load the model
  pid0 = [0.63 0.0504 1.9688] % Set initial values
  a1 = 3; a2 = 43;            % Initialize plant variables in model
  options = optimset('LargeScale','off','Display','iter',...
        'TolX',0.001,'TolFun',0.001);
  pid = lsqnonlin(@tracklsq, pid0, [], [], options, a1, a2)
  % Put variables back in the base workspace
  Kp = pid(1); Ki = pid(2); Kd = pid(3); 
  

The variable options passed to lsqnonlin defines the criteria and display characteristics. In this case you ask for output, use the medium-scale algorithm, and give termination tolerances for the step and objective function on the order of 0.001.

The optimization gives the solution for the proportional, integral, and derivative (Kp, Ki, Kd) gains of the controller after 64 function evaluations:

•                                                Directional 
  Iteration  Func-count  Residual    Step-size   derivative   Lambda
      1         3        8.66531          1        -3.48
      2        17        5.21602       85.4     -0.00813    0.0403059
      3        24        4.54036          1      -0.0331     0.393189
      4        31        4.47786      0.918     -0.00467     0.201985
      5        39        4.47552       2.12      0.00121     0.100992
      6        46        4.47524      0.203     -0.00193    0.0718569
      7        64        4.47524 -4.11e-007     -0.00157       2595.3
  Optimization terminated successfully: 
   Search direction less than tolX
  
  pid =
  
      2.9186    0.1398   12.6221
  
  

The resulting closed-loop step response is shown in Figure 2-4.

Figure 2-4: Closed-Loop Response Using lsqnonlin

Note    The call to sim results in a call to one of the Simulink ordinary differential equation (ODE) solvers. A choice must be made about the type of solver to use. From the optimization point of view, a fixed-step solver is the best choice if that is sufficient to solve the ODE. However, in the case of a stiff system, a variable-step method might be required to solve the ODE. The numerical solution produced by a variable-step solver, however, is not a smooth function of parameters, because of step-size control mechanisms. This lack of smoothness can prevent the optimization routine from converging. The lack of smoothness is not introduced when a fixed-step solver is used. (For a further explanation, see [1].) The Nonlinear Control Design Blockset is recommended for solving multiobjective optimization problems in conjunction with variable-step solvers in Simulink. It provides a special numeric gradient computation that works with Simulink and avoids introducing a problem of lack of smoothness.

Another solution approach is to use the fminimax function. In this case, rather than minimizing the error between the output and the input signal, you minimize the maximum value of the output at any time t between 0 and 100. Then in the function trackmmobj the objective function is simply the output yout returned by the sim command. But minimizing the maximum output at all time steps may force the output far below unity for some time steps. To keep the output above 0.95 after the first 20 seconds, in the constraint function trackkmmcon add a constraint yout >= 0.95 from t=20 to t=100. Because constraints must be in the form g <= 0, the constraint in the function is g = -yout(20:100)+.95.

Both trackmmobj and trackmmcon use the result yout from sim, calculated from the current pid values. The nonlinear constraint function is always called immediately after the objective function in fmincon, fminimax, fgoalattain, and fseminf with the same values. Thus you can avoid calling the simulation twice by using assignin to assign the current value of F to the variable F_TRACKMMOBJ in the base workspace. Then the first step in trackmmcon is to use evalin to evaluate the variable F_TRACKMMOBJ in the base workspace, and assign the result to F locally in trackmmcon.

Step 1: Write an M-file trackmmobj.m to compute objective function.

• function F = trackmmobj(pid,a1,a2)
  Kp = pid(1);
  Ki = pid(2);
  Kd = pid(3);
  % Compute function value
  opt = simset('solver','ode5','SrcWorkspace','Current');
  [tout,xout,yout] = sim('optsim',[0 100],opt);
  F = yout;
  assignin('base','F_TRACKMMOBJ',F);
  

Step 2: Write an M-file trackmmcon.m to compute nonlinear constraints.

• function [c,ceq] = trackmmcon(pid,a1,a2)
  F = evalin('base','F_TRACKMMOBJ');
  % Compute constraints
  c = -F(20:100)+.95;
  ceq = [ ];
  

Note that fminimax passes a1 and a2 to the objective and constraint values, so trackmmcon needs input arguments for these variables even though it does not use them.

Step 3: Invoke constrained optimization routine.

• optsim
  pid0 = [0.63 0.0504 1.9688]
  a1 = 3; a2 = 43;
  options = optimset('Display','iter',...
                     'TolX',0.001,'TolFun',0.001);
  pid = fminimax(@trackmmobj,pid0,[],[],[],[],[],[],...
                 'trackmmcon',options,a1,a2)
  % Put variables back in the base workspace
  Kp = pid(1); Ki = pid(2); Kd = pid(3); 
  

resulting in

•                    Max                 Directional 
  Iter F-count {F,constraints} Step-size derivative  Procedure
   1    11        1.264          1         1.18   
   2    17        1.055          1       -0.172   
   3    23        1.004          1      -0.0128   Hessian modified twice
   4    29       0.9997          1    3.48e-005   Hessian modified
   5    35       0.9996          1   -1.36e-006   Hessian modified twice
  
  Optimization terminated successfully:
   Search direction less than 2*options.TolX and
    maximum constraint violation is less than options.TolCon
  Active Constraints:
       1
      14
     182
  
  pid =
      0.5894    0.0605    5.5295
  

The last value shown in the MAX{F,constraints} column of the output shows that the maximum value for all the time steps is 0.9996. The closed loop response with this result is shown in Figure 2-5, Closed-Loop Response Using fminimax.

This solution differs from the lsqnonlin solution, because you are solving different problem formulations.

Figure 2-5: Closed-Loop Response Using fminimax

Signal Processing Example

Consider designing a linear-phase Finite Impulse Response (FIR) filter. The problem is to design a lowpass filter with magnitude one at all frequencies between 0 and 0.1 Hz and magnitude zero between 0.15 and 0.5 Hz.

The frequency response H(f) for such a filter is defined by

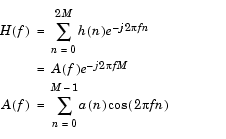
(2-6)

where A(f) is the magnitude of the frequency response. One solution is to apply a goal attainment method to the magnitude of the frequency response. Given a function that computes the magnitude, the function fgoalattain will attempt to vary the magnitude coefficients a(n) until the magnitude response matches the desired response within some tolerance. The function that computes the magnitude response is given in filtmin.m. This function takes a, the magnitude function coefficients, and w, the discretization of the frequency domain we are interested in.

To set up a goal attainment problem, you must specify the goal and weights for the problem. For frequencies between 0 and 0.1, the goal is one. For frequencies between 0.15 and 0.5, the goal is zero. Frequencies between 0.1 and 0.15 are not specified, so no goals or weights are needed in this range.

This information is stored in the variable goal passed to fgoalattain. The length of goal is the same as the length returned by the function filtmin. So that the goals are equally satisfied, usually weight would be set to abs(goal). However, since some of the goals are zero, the effect of using weight=abs(goal) will force the objectives with weight 0 to be satisfied as hard constraints, and the objectives with weight 1 possibly to be underattained (see Goal Attainment Method). Because all the goals are close in magnitude, using a weight of unity for all goals will give them equal priority. (Using abs(goal) for the weights is more important when the magnitude of goal differs more significantly.) Also, setting

• options = optimset('GoalsExactAchieve',length(goal)); 
  

specifies that each objective should be as near as possible to its goal value (neither greater nor less than).

Step 1: Write an M-file filtmin.m.

• function y = filtmin(a,w)
  n = length(a);
  y = cos(w'*(0:n-1)*2*pi)*a ;
  

Step 2: Invoke optimization routine.

• % Plot with initial coefficients
  a0 = ones(15,1);
  incr = 50;
  w = linspace(0,0.5,incr);
  
  y0 = filtmin(a0,w);
  clf, plot(w,y0.'-:');
  drawnow;
  
  % Set up the goal attainment problem
  w1 = linspace(0,0.1,incr) ;
  w2 = linspace(0.15,0.5,incr);
  w0 = [w1 w2];
  goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))];
  weight = ones(size(goal)); 
  
  % Call fgoalattain
  options = optimset('GoalsExactAchieve',length(goal));
  [a,fval,attainfactor,exitflag] = fgoalattain(@filtmin,...
      a0,goal,weight,[],[],[],[],[],[],[],options,w0);
  
  % Plot with the optimized (final) coefficients
  y = filtmin(a,w);
  hold on, plot(w,y,'r')
  axis([0 0.5 -3 3])
  xlabel('Frequency (Hz)')
  ylabel('Magnitude Response (dB)')
  legend('initial', 'final')
  grid on
  

Compare the magnitude response computed with the initial coefficients and the final coefficients (Figure 2-6). Note that you could use the remez function in the Signal Processing Toolbox to design this filter.

Figure 2-6: Magnitude Response with Initial and Final Magnitude Coefficients

Nonlinear Equations with Finite-Difference Jacobian

Large-Scale Examples