Optimization Toolbox

fgoalattain

Solve multiobjective goal attainment problem

where x, weight, goal, b, beq, lb, and ub are vectors, A and Aeq are matrices, and c(x), ceq(x), and F(x) are functions that return vectors. F(x), c(x), and ceq(x) can be nonlinear functions.

Syntax

• x = fgoalattain(fun,x0,goal,weight)
  x = fgoalattain(fun,x0,goal,weight,A,b)
  x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq)
  x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub)
  x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon)
  x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,...
                  lb,ub,nonlcon,options)
  x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,...
                  lb,ub,nonlcon,options,P1,P2,...)
  [x,fval] = fgoalattain(...)
  [x,fval,attainfactor] = fgoalattain(...)
  [x,fval,attainfactor,exitflag] = fgoalattain(...)
  [x,fval,attainfactor,exitflag,output] = fgoalattain(...)
  [x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...)
  

Description

fgoalattain solves the goal attainment problem, which is one formulation for minimizing a multiobjective optimization problem.

x = fgoalattain(fun,x0,goal,weight) tries to make the objective functions supplied by fun attain the goals specified by goal by varying x, starting at x0, with weight specified by weight.

x = fgoalattain(fun,x0,goal,weight,A,b) solves the goal attainment problem subject to the linear inequalities A*x <= b.

x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq) solves the goal attainment problem subject to the linear equalities Aeq*x = beq as well. Set A=[] and b=[] if no inequalities exist.

x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that the solution is always in the range lb <= x <= ub.

x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) subjects the goal attainment problem to the nonlinear inequalities c(x) or nonlinear equality constraints ceq(x) defined in nonlcon. fgoalattain optimizes such that c(x) <= 0 and ceq(x) = 0. Set lb=[] and/or ub=[] if no bounds exist.

x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,... options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,... options,P1,P2,...) passes the problem-dependent parameters P1, P2, etc., directly to the functions fun and nonlcon. Pass empty matrices as placeholders for A, b, Aeq, beq, lb, ub, nonlcon, and options if these arguments are not needed.

[x,fval] = fgoalattain(...) returns the values of the objective functions computed in fun at the solution x.

[x,fval,attainfactor] = fgoalattain(...) returns the attainment factor at the solution x.

[x,fval,attainfactor,exitflag] = fgoalattain(...) returns a value exitflag that describes the exit condition of fgoalattain.

[x,fval,attainfactor,exitflag,output] = fgoalattain(...) returns a structure output that contains information about the optimization.

[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(...) returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to fgoalattain. This section provides function-specific details for fun, goal, nonlcon, options, and weight:

fun	The function to be minimized. fun is a function that accepts a vector x and returns a vector F, the objective functions evaluated at x. The function fun can be specified as a function handle. x = fgoalattain(@myfun,x0,goal,weight) where myfun is a MATLAB function such as function F = myfun(x) F = ... % Compute function values at x. fun can also be an inline object. x = fgoalattain(inline('sin(x.*x)'),x0,goal,weight); To make an objective function as near as possible to a goal value, (i.e., neither greater than nor less than) use optimset to set the GoalsExactAchieve parameter to the number of objectives required to be in the neighborhood of the goal values. Such objectives must be partitioned into the first elements of the vector F returned by fun. If the gradient of the objective function can also be computed and the GradObj parameter is 'on', as set by options = optimset('GradObj','on') then the function fun must return, in the second output argument, the gradient value G, a matrix, at x. Note that by checking the value of nargout the function can avoid computing G when fun is called with only one output argument (in the case where the optimization algorithm only needs the value of F but not G). function [F,G] = myfun(x) F = ...            % Compute the function values at x if nargout > 1     % Two output arguments    G = ...         % Gradients evaluated at x end
	The gradient consists of the partial derivative dF/dx of each F at the point x. If F is a vector of length m and x has length n, where n is the length of x0, then the gradient G of F(x) is an n-by-m matrix where G(i,j) is the partial derivative of F(j) with respect to x(i) (i.e., the jth column of G is the gradient of the jth objective function F(j)).
goal	Vector of values that the objectives attempt to attain. The vector is the same length as the number of objectives F returned by fun. fgoalattain attempts to minimize the values in the vector F to attain the goal values given by goal.
nonlcon	The function that computes the nonlinear inequality constraints c(x) <= 0 and the nonlinear equality constraints ceq(x) = 0. The function nonlcon accepts a vector x and returns two vectors c and ceq. The vector c contains the nonlinear inequalities evaluated at x, and ceq contains the nonlinear equalities evaluated at x. The function nonlcon can be specified as a function handle. x = fgoalattain(@myfun,x0,goal,weight,A,b,Aeq,beq,... lb,ub,@mycon) where mycon is a MATLAB function such as function [c,ceq] = mycon(x) c = ... % compute nonlinear inequalities at x. ceq = ... % compute nonlinear equalities at x. If the gradients of the constraints can also be computed and the GradConstr parameter is 'on', as set by options = optimset('GradConstr','on') then the function nonlcon must also return, in the third and fourth output arguments, GC, the gradient of c(x), and GCeq, the gradient of ceq(x). Note that by checking the value of nargout the function can avoid computing GC and GCeq when nonlcon is called with only two output arguments (in the case where the optimization algorithm only needs the values of c and ceq but not GC and GCeq).
	function [c,ceq,GC,GCeq] = mycon(x) c = ...              % Nonlinear inequalities at x ceq = ...            % Nonlinear equalities at x if nargout > 2       % Nonlcon called with 4 outputs    GC = ...          % Gradients of the inequalities    GCeq = ...        % Gradients of the equalities end If nonlcon returns a vector c of m components and x has length n, where n is the length of x0, then the gradient GC of c(x) is an n-by-m matrix, where GC(i,j) is the partial derivative of c(j) with respect to x(i) (i.e., the jth column of GC is the gradient of the jth inequality constraint c(j)). Likewise, if ceq has p components, the gradient GCeq of ceq(x) is an n-by-p matrix, where GCeq(i,j) is the partial derivative of ceq(j) with respect to x(i) (i.e., the jth column of GCeq is the gradient of the jth equality constraint ceq(j)).
options	Options provides the function-specific details for the options parameters.
weight	A weighting vector to control the relative under-attainment or over-attainment of the objectives in fgoalattain. When the values of goal are all nonzero, to ensure the same percentage of under- or over-attainment of the active objectives, set the weighting function to abs(goal). (The active objectives are the set of objectives that are barriers to further improvement of the goals at the solution.) Note    Setting weight=abs(goal) when any of the goal values are zero causes that goal constraint to be treated like a hard constraint rather than as a goal constraint.
	When the weighting function weight is positive, fgoalattain attempts to make the objectives less than the goal values. To make the objective functions greater than the goal values, set weight to be negative rather than positive. To make an objective function as near as possible to a goal value, use the GoalsExactAchieve parameter and put that objective as the first element of the vector returned by fun (see the description of fun and options above).

Output Arguments

Function Arguments contains general descriptions of arguments returned by fgoalattain. This section provides function-specific details for attainfactor, exitflag, lambda, and output:

attainfactor	The amount of over- or underachievement of the goals. If attainfactor is negative, the goals have been over-achieved; if attainfactor is positive, the goals have been under-achieved.
exitflag	Describes the exit condition:
	> 0	The function converged to a solution x.
	0	The maximum number of function evaluations or iterations was exceeded.
	< 0	The function did not converge to a solution.
lambda	Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields of the structure are:
	lower	Lower bounds lb
	upper	Upper bounds ub
	ineqlin	Linear inequalities
	eqlin	Linear equalities
	ineqnonlin	Nonlinear inequalities
	eqnonlin	Nonlinear equalities
output	Structure containing information about the optimization. The fields of the structure are:
	iterations	Number of iterations taken.
	funcCount	Number of function evaluations.
	algorithm	Algorithm used.

Options

Optimization options parameters used by fgoalattain. You can use optimset to set or change the values of these fields in the parameters structure, options. See Optimization Parameters, for detailed information:

DerivativeCheck	Compare user-supplied derivatives (gradients of objective or constraints) to finite-differencing derivatives.
Diagnostics	Print diagnostic information about the function to be minimized or solved.
DiffMaxChange	Maximum change in variables for finite-difference gradients.
DiffMinChange	Minimum change in variables for finite-difference gradients.
Display	Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output.
GoalsExactAchieve	Specifies the number of goals to "just" achieve, that is, do not try to over- or underachieve.
GradConstr	Gradient for the constraints defined by user. See the description of nonlcon above to see how to define the gradient in nonlcon
GradObj	Gradient for the objective function defined by user. See the description of fun above to see how to define the gradient in fun. The gradient must be provided to use the large-scale method. It is optional for the medium-scale method.
MaxFunEvals	Maximum number of function evaluations allowed.
MaxIter	Maximum number of iterations allowed.
MeritFunction	Use goal attainment/minimax merit function if set to 'multiobj'. Use fmincon merit function if set to 'singleobj'.
TolCon	Termination tolerance on the constraint violation.
TolFun	Termination tolerance on the function value.
TolX	Termination tolerance on x.

Examples

Consider a linear system of differential equations.

An output feedback controller, K, is designed producing a closed loop system

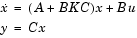
The eigenvalues of the closed loop system are determined from the matrices A, B, C, and K using the command eig(A+B*K*C). Closed loop eigenvalues must lie on the real axis in the complex plane to the left of the points [-5,-3,-1]. In order not to saturate the inputs, no element in K can be greater than 4 or be less than -4.

The system is a two-input, two-output, open loop, unstable system, with state-space matrices.

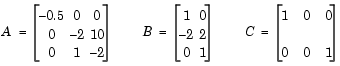
The set of goal values for the closed loop eigenvalues is initialized as

•  goal = [-5,-3,-1];
  

To ensure the same percentage of under- or over-attainment in the active objectives at the solution, the weighting matrix, weight, is set to abs(goal).

Starting with a controller, K = [-1,-1; -1,-1], first write an M-file, eigfun.m.

• function F = eigfun(K,A,B,C)
  F = sort(eig(A+B*K*C)); % Evaluate objectives
  

Next, enter system matrices and invoke an optimization routine.

• A = [-0.5 0 0; 0 -2 10; 0 1 -2];
  B = [1 0; -2 2; 0 1];
  C = [1 0 0; 0 0 1]; 
  K0 = [-1 -1; -1 -1];       % Initialize controller matrix
  goal = [-5 -3 -1];         % Set goal values for the eigenvalues
  weight = abs(goal)         % Set weight for same percentage
  lb = -4*ones(size(K0));    % Set lower bounds on the controller
  ub = 4*ones(size(K0));     % Set upper bounds on the controller
  options = optimset('Display','iter');   % Set display parameter
  [K,fval,attainfactor] = fgoalattain(@eigfun,K0,... 
      goal,weight,[],[],[],[],lb,ub,[],options,A,B,C)
  

This example can be run by using the demonstration script goaldemo. After about 12 iterations, a solution is

• Active constraints:
       1
       2
       4
       9
      10
  K = 
      -4.0000    -0.2564
      -4.0000    -4.0000
  
  fval =
      -6.9313
      -4.1588
      -1.4099
  
  attainfactor = 
      -0.3863
  

Discussion

The attainment factor indicates that each of the objectives has been over-achieved by at least 38.63% over the original design goals. The active constraints, in this case constraints 1 and 2, are the objectives that are barriers to further improvement and for which the percentage of over-attainment is met exactly. Three of the lower bound constraints are also active.

In the above design, the optimizer tries to make the objectives less than the goals. For a worst case problem where the objectives must be as near to the goals as possible, use optimset to set the GoalsExactAchieve parameter to the number of objectives for which this is required.

Consider the above problem when you want all the eigenvalues to be equal to the goal values. A solution to this problem is found by invoking fgoalattain with the GoalsExactAchieve parameter set to 3.

• options = optimset('GoalsExactAchieve',3);
  [K,fval,attainfactor] = fgoalattain(...
     @eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options,A,B,C)
  

After about seven iterations, a solution is

• K = 
      -1.5954    1.2040
      -0.4201   -2.9046
  
  fval =
      -5.0000
      -3.0000
      -1.0000
  
  attainfactor = 
       1.0859e-20
  

In this case the optimizer has tried to match the objectives to the goals. The attainment factor (of 1.0859e-20) indicates that the goals have been matched almost exactly.

Notes

This problem has discontinuities when the eigenvalues become complex; this explains why the convergence is slow. Although the underlying methods assume the functions are continuous, the method is able to make steps toward the solution since the discontinuities do not occur at the solution point. When the objectives and goals are complex, fgoalattain tries to achieve the goals in a least-squares sense.

Algorithm

Multiobjective optimization concerns the minimization of a set of objectives simultaneously. One formulation for this problem, and implemented in fgoalattain, is the goal attainment problem of Gembicki[3]. This entails the construction of a set of goal values for the objective functions. Multiobjective optimization is discussed fully in the Standard Algorithms chapter.

In this implementation, the slack variable 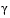is used as a dummy argument to minimize the vector of objectives F(x) simultaneously; goal is a set of values that the objectives attain. Generally, prior to the optimization, it is unknown whether the objectives will reach the goals (under attainment) or be minimized less than the goals (over attainment). A weighting vector, weight, controls the relative under-attainment or over-attainment of the objectives.

fgoalattain uses a Sequential Quadratic Programming (SQP) method, which is described fully in the Standard Algorithms chapter. Modifications are made to the line search and Hessian. In the line search an exact merit function (see [1] and [4]) is used together with the merit function proposed by [5], [6]. The line search is terminated when either merit function shows improvement. A modified Hessian, which takes advantage of special structure of this problem, is also used (see [1] and [[4]). A full description of the modifications used is found in Goal Attainment Method in "Introduction to Algorithms." Setting the MeritFunction parameter to'singleobj' with

• options = optimset(options,'MeritFunction','singleobj')
  

uses the merit function and Hessian used in fmincon.

attainfactor contains the value of 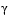at the solution. A negative value of 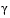indicates over-attainment in the goals.

See also SQP Implementation for more details on the algorithm used and the types of procedures printed under the Procedures heading when the Display parameter is set to 'iter'.

Limitations

The objectives must be continuous. fgoalattain may give only local solutions.

See Also

@ (function_handle), fmincon, fminimax, optimset

References

[1]  Brayton, R.K., S.W. Director, G.D. Hachtel, and L.Vidigal, "A New Algorithm for Statistical Circuit Design Based on Quasi-Newton Methods and Function Splitting," IEEE Transactions on Circuits and Systems, Vol. CAS-26, pp. 784-794, Sept. 1979.

[2]  Fleming, P.J. and A.P. Pashkevich, Computer Aided Control System Design Using a Multi-Objective Optimisation Approach, Control 1985 Conference, Cambridge, UK, pp. 174-179.

[3]  Gembicki, F.W., "Vector Optimization for Control with Performance and Parameter Sensitivity Indices," Ph.D. Dissertation, Case Western Reserve Univ., Cleveland, OH, 1974.

[4]  Grace, A.C.W., "Computer-Aided Control System Design Using Optimization Techniques," Ph.D. Thesis, University of Wales, Bangor, Gwynedd, UK, 1989.

[5]  Han, S.P., "A Globally Convergent Method For Nonlinear Programming," Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.

[6]  Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations," Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.

Functions - Alphabetical List

fminbnd