fminimax (Optimization Toolbox)

Solve the minimax problem

where x, b, beq, lb, and ub are vectors, A and Aeq are matrices, c(x), ceq(x), and F(x) are functions that return vectors. F(x), c(x), and ceq(x) can be nonlinear functions.

Syntax

x = fminimax(fun,x0)
x = fminimax(fun,x0,A,b)
x = fminimax(fun,x0,A,b,Aeq,beq)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...)
[x,fval] = fminimax(...)
[x,fval,maxfval] = fminimax(...)
[x,fval,maxfval,exitflag] = fminimax(...)
[x,fval,maxfval,exitflag,output] = fminimax(...)
[x,fval,maxfval,exitflag,output,lambda] = fminimax(...)

Description

fminimax minimizes the worst-case value of a set of multivariable functions, starting at an initial estimate. The values may be subject to constraints. This is generally referred to as the minimax problem.

x = fminimax(fun,x0) starts at x0 and finds a minimax solution x to the functions described in fun.

x = fminimax(fun,x0,A,b) solves the minimax problem subject to the linear inequalities A*x <= b.

x = fminimax(fun,x,A,b,Aeq,beq) solves the minimax problem subject to the linear equalities Aeq*x = beq as well. Set A=[] and b=[] if no inequalities exist.

x = fminimax(fun,x,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that the solution is always in the range lb <= x <= ub.

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) subjects the minimax problem to the nonlinear inequalities c(x) or equality constraints ceq(x) defined in nonlcon. fminimax optimizes such that c(x) <= 0 and ceq(x) = 0. Set lb=[] and/or ub=[] if no bounds exist.

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...) passes the problem-dependent parameters P1, P2, etc., directly to the functions fun and nonlcon. Pass empty matrices as placeholders for A, b, Aeq, beq, lb, ub, nonlcon, and options if these arguments are not needed.

[x,fval] = fminimax(...) returns the value of the objective function fun at the solution x.

[x,fval,maxfval] = fminimax(...) returns the maximum function value at the solution x.

[x,fval,maxfval,exitflag] = fminimax(...) returns a value exitflag that describes the exit condition of fminimax.

[x,fval,maxfval,exitflag,output] = fminimax(...) returns a structure output with information about the optimization.

[x,fval,maxfval,exitflag,output,lambda] = fminimax(...) returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to fminimax. This section provides function-specific details for fun, nonlcon, and options:

fun
The function to be minimized. fun is a function that accepts a vector x and returns a vector F, the objective functions evaluated at x. The function fun can be specified as a function handle.
x = fminimax(@myfun,x0)
where myfun is a MATLAB function such as
function F = myfun(x) F = ...            % Compute function values at x
fun can also be an inline object.
x = fminimax(inline('sin(x.*x)'),x0);
To minimize the worst case absolute values of any of the elements of the vector F(x) (i.e., min{max abs{F(x)} } ), partition those objectives into the first elements of F and use optimset to set the MinAbsMax parameter to be the number of such objectives.
If the gradient of the objective function can also be computed and the GradObj parameter is 'on', as set by
options = optimset('GradObj','on')
then the function fun must return, in the second output argument, the gradient value G, a matrix, at x. Note that by checking the value of nargout the function can avoid computing G when myfun is called with only one output argument (in the case where the optimization algorithm only needs the value of F but not G).
function [F,G] = myfun(x) F = ...          % Compute the function values at x if nargout > 1   % Two output arguments    G = ...       % Gradients evaluated at x end

The gradient consists of the partial derivative dF/dx of each F at the point x. If F is a vector of length m and x has length n, where n is the length of x0, then the gradient G of F(x) is an n-by-m matrix where G(i,j) is the partial derivative of F(j) with respect to x(i) (i.e., the jth column of G is the gradient of the jth objective function F(j)).

nonlcon
The function that computes the nonlinear inequality constraints c(x) <= 0 and nonlinear equality constraints ceq(x) = 0. The function nonlcon accepts a vector x and returns two vectors c and ceq. The vector c contains the nonlinear inequalities evaluated at x, and ceq contains the nonlinear equalities evaluated at x. The function nonlcon can be specified as a function handle.
x = fminimax(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)
where mycon is a MATLAB function such as
function [c,ceq] = mycon(x) c = ...     % Compute nonlinear inequalities at x ceq = ...   % Compute nonlinear equalities at x
If the gradients of the constraints can also be computed and the GradConstr parameter is 'on', as set by
options = optimset('GradConstr','on')
then the function nonlcon must also return, in the third and fourth output arguments, GC, the gradient of c(x), and GCeq, the gradient of ceq(x). Note that by checking the value of nargout the function can avoid computing GC and GCeq when nonlcon is called with only two output arguments (in the case where the optimization algorithm only needs the values of c and ceq but not GC and GCeq).
function [c,ceq,GC,GCeq] = mycon(x) c = ...          % Nonlinear inequalities at x ceq = ...        % Nonlinear equalities at x if nargout > 2   % nonlcon called with 4 outputs    GC = ...      % Gradients of the inequalities    GCeq = ...    % Gradients of the equalities end

If nonlcon returns a vector c of m components and x has length n, where n is the length of x0, then the gradient GC of c(x) is an n-by-m matrix, where GC(i,j) is the partial derivative of c(j) with respect to x(i) (i.e., the jth column of GC is the gradient of the jth inequality constraint c(j)). Likewise, if ceq has p components, the gradient GCeq of ceq(x) is an n-by-p matrix, where GCeq(i,j) is the partial derivative of ceq(j) with respect to x(i) (i.e., the jth column of GCeq is the gradient of the jth equality constraint ceq(j)).

options
Options provides the function-specific details for the options parameters.

`fun`	The function to be minimized. `fun` is a function that accepts a vector `x` and returns a vector `F`, the objective functions evaluated at `x`. The function `fun` can be specified as a function handle. x = fminimax(@myfun,x0) where `myfun` is a MATLAB function such as function F = myfun(x) F = ... % Compute function values at x `fun` can also be an inline object. x = fminimax(inline('sin(x.x)'),x0); To minimize the worst case absolute values of any of the elements of the vector F(x)* (i.e., min{max abs{F(x)} } ), partition those objectives into the first elements of `F` and use `optimset` to set the `MinAbsMax` parameter to be the number of such objectives. If the gradient of the objective function can also be computed and the `GradObj` parameter is `'on'`, as set by options = optimset('GradObj','on') then the function `fun` must return, in the second output argument, the gradient value `G`, a matrix, at `x`. Note that by checking the value of `nargout` the function can avoid computing `G` when `myfun` is called with only one output argument (in the case where the optimization algorithm only needs the value of `F` but not `G`). function [F,G] = myfun(x) F = ... % Compute the function values at x if nargout > 1 % Two output arguments G = ... % Gradients evaluated at x end
	The gradient consists of the partial derivative dF/dx of each `F` at the point `x`. If `F` is a vector of length `m` and `x` has length `n`, where `n` is the length of `x0`, then the gradient `G` of `F(x)` is an n-by-m matrix where `G(i,j)` is the partial derivative of `F(j)` with respect to `x(i)` (i.e., the `j`th column of `G` is the gradient of the `j`th objective function `F(j)`).
`nonlcon`	The function that computes the nonlinear inequality constraints `c(x) <= 0` and nonlinear equality constraints `ceq(x) = 0`. The function `nonlcon` accepts a vector `x` and returns two vectors `c` and `ceq`. The vector `c` contains the nonlinear inequalities evaluated at `x`, and `ceq` contains the nonlinear equalities evaluated at `x`. The function `nonlcon` can be specified as a function handle. x = fminimax(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon) where `mycon` is a MATLAB function such as function [c,ceq] = mycon(x) c = ... % Compute nonlinear inequalities at x ceq = ... % Compute nonlinear equalities at x If the gradients of the constraints can also be computed and the `GradConstr` parameter is `'on'`, as set by options = optimset('GradConstr','on') then the function `nonlcon` must also return, in the third and fourth output arguments, `GC`, the gradient of `c(x)`, and `GCeq`, the gradient of `ceq(x)`. Note that by checking the value of `nargout` the function can avoid computing `GC` and `GCeq` when `nonlcon` is called with only two output arguments (in the case where the optimization algorithm only needs the values of `c` and `ceq` but not `GC` and `GCeq`). function [c,ceq,GC,GCeq] = mycon(x) c = ... % Nonlinear inequalities at x ceq = ... % Nonlinear equalities at x if nargout > 2 % nonlcon called with 4 outputs GC = ... % Gradients of the inequalities GCeq = ... % Gradients of the equalities end
	If `nonlcon` returns a vector `c` of `m` components and `x` has length `n`, where `n` is the length of `x0`, then the gradient `GC` of `c(x)` is an n-by-m matrix, where `GC(i,j)` is the partial derivative of `c(j)` with respect to `x(i)` (i.e., the `j`th column of `GC` is the gradient of the `j`th inequality constraint `c(j)`). Likewise, if `ceq` has `p` components, the gradient `GCeq` of `ceq(x)` is an n-by-p matrix, where `GCeq(i,j)` is the partial derivative of `ceq(j)` with respect to `x(i)` (i.e., the `j`th column of `GCeq` is the gradient of the `j`th equality constraint `ceq(j)`).
`options`	Options provides the function-specific details for the `options` parameters.

Output Arguments

Function Arguments contains general descriptions of arguments returned by fminimax. This section provides function-specific details for exitflag, lambda, maxfval, and output:

exitflag
Describes the exit condition:

> 0
The function converged to a solution x.

0
The maximum number of function evaluations or iterations was exceeded.

< 0
The function did not converge to a solution.

lambda
Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields of the structure are:

lower
Lower bounds lb

upper
Upper bounds ub

ineqlin
Linear inequalities

eqlin
Linear equalities

ineqnonlin
Nonlinear inequalities

eqnonlin
Nonlinear equalities

maxfval
Maximum of the function values evaluated at the solution x, that is, maxfval = max{fun(x)}.

output
Structure containing information about the optimization. The fields of the structure are:

iterations
Number of iterations taken.

funcCount
Number of function evaluations.

algorithm
Algorithm used.

`exitflag`	Describes the exit condition:
	> 0	The function converged to a solution `x`.
	0	The maximum number of function evaluations or iterations was exceeded.
	< 0	The function did not converge to a solution.
`lambda`	Structure containing the Lagrange multipliers at the solution `x` (separated by constraint type). The fields of the structure are:
	`lower`	Lower bounds `lb`
	`upper`	Upper bounds `ub`
	`ineqlin`	Linear inequalities
	`eqlin`	Linear equalities
	`ineqnonlin`	Nonlinear inequalities
	`eqnonlin`	Nonlinear equalities
`maxfval`	Maximum of the function values evaluated at the solution `x`, that is, `maxfval = max{fun(x)}`.
`output`	Structure containing information about the optimization. The fields of the structure are:
	`iterations`	Number of iterations taken.
	`funcCount`	Number of function evaluations.
	`algorithm`	Algorithm used.

Options

Optimization options parameters used by fminimax. You can use optimset to set or change the values of these fields in the parameters structure, options. See Optimization Parameters, for detailed information:

DerivativeCheck
Compare user-supplied derivatives (gradients of the objective or constraints) to finite-differencing derivatives.

Diagnostics
Print diagnostic information about the function to be minimized or solved.

DiffMaxChange
Maximum change in variables for finite-difference gradients.

DiffMinChange
Minimum change in variables for finite-difference gradients.

Display
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output.

GradConstr
Gradient for the constraints defined by user. See the description of nonlcon above to see how to define the gradient in nonlcon.

GradObj
Gradient for the objective function defined by user. See the description of fun above to see how to define the gradient in fun. The gradient must be provided to use the large-scale method. It is optional for the medium-scale method.

MaxFunEvals
Maximum number of function evaluations allowed.

MaxIter
Maximum number of iterations allowed.

MeritFunction
Use goal attainment/minimax merit function if set to 'multiobj'. Use fmincon merit function if set to 'singleobj'.

MinAbsMax
Number of F(x) to minimize the worst case absolute values.

TolCon
Termination tolerance on the constraint violation.

TolFun
Termination tolerance on the function value.

TolX
Termination tolerance on x.

`DerivativeCheck`	Compare user-supplied derivatives (gradients of the objective or constraints) to finite-differencing derivatives.
`Diagnostics`	Print diagnostic information about the function to be minimized or solved.
`DiffMaxChange`	Maximum change in variables for finite-difference gradients.
`DiffMinChange`	Minimum change in variables for finite-difference gradients.
`Display`	Level of display. `'off'` displays no output; `'iter'` displays output at each iteration; `'final'` (default) displays just the final output.
`GradConstr`	Gradient for the constraints defined by user. See the description of `nonlcon` above to see how to define the gradient in `nonlcon`.
`GradObj`	Gradient for the objective function defined by user. See the description of `fun` above to see how to define the gradient in `fun`. The gradient must be provided to use the large-scale method. It is optional for the medium-scale method.
`MaxFunEvals`	Maximum number of function evaluations allowed.
`MaxIter`	Maximum number of iterations allowed.
`MeritFunction`	Use goal attainment/minimax merit function if set to `'multiobj`'. Use `fmincon` merit function if set to `'singleobj'`.
`MinAbsMax`	Number of F(x) to minimize the worst case absolute values.
`TolCon`	Termination tolerance on the constraint violation.
`TolFun`	Termination tolerance on the function value.
`TolX`	Termination tolerance on `x`.

Examples

Find values of x that minimize the maximum value of

where

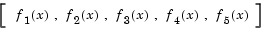
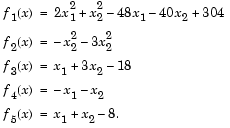
First, write an M-file that computes the five functions at x.

function f = myfun(x)
f(1)= 2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304;     % Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1)- x(2);
f(5)= x(1) + x(2) - 8;

Next, invoke an optimization routine.

x0 = [0.1; 0.1];       % Make a starting guess at solution
[x,fval] = fminimax(@myfun,x0)

After seven iterations, the solution is

x = 
     4.0000
     4.0000
fval =
     0.0000  -64.0000  -2.0000  -8.0000  -0.0000

Notes

The number of objectives for which the worst case absolute values of F are minimized is set in the MinAbsMax parameter using optimset. Such objectives should be partitioned into the first elements of F.

For example, consider the above problem, which requires finding values of x that minimize the maximum absolute value of

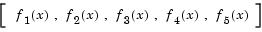
This is solved by invoking fminimax with the commands

x0 = [0.1; 0.1];        % Make a starting guess at the solution
options = optimset('MinAbsMax',5);   % Minimize absolute values
[x,fval] = fminimax(@myfun,x0,[],[],[],[],[],[],[],options);

After seven iterations, the solution is

x = 
     4.9256
     2.0796
fval = 
    37.2356 -37.2356 -6.8357 -7.0052 -0.9948

If equality constraints are present and dependent equalities are detected and removed in the quadratic subproblem, 'dependent' is printed under the Procedures heading (when the Display parameter is set to 'iter'). The dependent equalities are only removed when the equalities are consistent. If the system of equalities is not consistent, the subproblem is infeasible and 'infeasible' is printed under the Procedures heading.

Algorithm

fminimax uses a Sequential Quadratic Programming (SQP) method [1]. Modifications are made to the line search and Hessian. In the line search an exact merit function (see [2] and [4]) is used together with the merit function proposed by [3] and [5]. The line search is terminated when either merit function shows improvement. A modified Hessian that takes advantage of special structure of this problem is also used. Using optimset to set the MeritFunction parameter to'singleobj' uses the merit function and Hessian used in fmincon.

See also SQP Implementation for more details on the algorithm used and the types of procedures printed under the Procedures heading when the Display parameter is set to'iter'.

Limitations

The function to be minimized must be continuous. fminimax may only give local solutions.

See Also

@ (function_handle), fgoalattain, lsqnonlin, optimset

References

[1] Brayton, R.K., S.W. Director, G.D. Hachtel, and L.Vidigal, "A New Algorithm for Statistical Circuit Design Based on Quasi-Newton Methods and Function Splitting," IEEE Trans. Circuits and Systems, Vol. CAS-26, pp. 784-794, Sept. 1979.

[2] Grace, A.C.W., "Computer-Aided Control System Design Using Optimization Techniques," Ph.D. Thesis, University of Wales, Bangor, Gwynedd, UK, 1989.

[3] Han, S.P., "A Globally Convergent Method For Nonlinear Programming," Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.

[4] Madsen, K. and H. Schjaer-Jacobsen, "Algorithms for Worst Case Tolerance Optimization," IEEE Transactions of Circuits and Systems, Vol. CAS-26, Sept. 1979.

[5] Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations," Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.

fmincon fminsearch