lsqnonlin (Optimization Toolbox)

Solve nonlinear least-squares (nonlinear data-fitting) problem

where L is a constant.

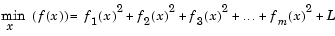
Syntax

x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options)
x = lsqnonlin(fun,x0,eb,ub,options,P1,P2, ... )
[x,resnorm] = lsqnonlin(...)
[x,resnorm,residual] = lsqnonlin(...)
[x,resnorm,residual,exitflag] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] =
    lsqnonlin(...)

Description

lsqnonlin solves nonlinear least-squares problems, including nonlinear data-fitting problems.

Rather than compute the value f(x) (the "sum of squares"), lsqnonlin requires the user-defined function to compute the vector-valued function

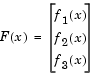
Then, in vector terms, this optimization problem may be restated as

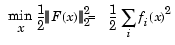
where x is a vector and F(x) is a function that returns a vector value.

x = lsqnonlin(fun,x0) starts at the point x0 and finds a minimum to the sum of squares of the functions described in fun. fun should return a vector of values and not the sum-of-squares of the values. (fun(x) is summed and squared implicitly in the algorithm.)

x = lsqnonlin(fun,x0,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that the solution is always in the range lb <= x <= ub.

x = lsqnonlin(fun,x0,lb,ub,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters. Pass empty matrices for lb an ub if no bounds exist.

x = lsqnonlin(fun,x0,lb,ub,options,P1,P2,...) passes the problem-dependent parameters P1, P2, etc., directly to the function fun. Pass an empty matrix for options to use the default values for options.

[x,resnorm] = lsqnonlin(...) returns the value of the squared 2-norm of the residual at x: sum(fun(x).^2).

[x,resnorm,residual] = lsqnonlin(...) returns the value of the residual, fun(x), at the solution x.

[x,resnorm,residual,exitflag] = lsqnonlin(...) returns a value exitflag that describes the exit condition.

[x,resnorm,residual,exitflag,output] = lsqnonlin(...) returns a structure output that contains information about the optimization.

[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...) returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.

[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(...) returns the Jacobian of fun at the solution x.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to lsqnonlin. This section provides function-specific details for fun and options:

fun
The function whose sum-of-squares is minimized. fun is a function that accepts a vector x and returns a vector F, the objective functions evaluated at x. The function fun can be specified as a function handle.
x = lsqnonlin(@myfun,x0)
where myfun is a MATLAB function such as
function F = myfun(x) F = ... % Compute function values at x
fun can also be an inline object.
x = lsqnonlin(inline('sin(x.*x)'),x0);
If the Jacobian can also be computed and the Jacobian parameter is 'on', set by
options = optimset('Jacobian','on')
then the function fun must return, in a second output argument, the Jacobian value J, a matrix, at x. Note that by checking the value of nargout the function can avoid computing J when fun is called with only one output argument (in the case where the optimization algorithm only needs the value of F but not J).
function [F,J] = myfun(x) F = ... % Objective function values at x if nargout > 1 % Two output arguments J = ... % Jacobian of the function evaluated at x end
If fun returns a vector (matrix) of m components and x has length n, where n is the length of x0, then the Jacobian J is an m-by-n matrix where J(i,j) is the partial derivative of F(i) with respect to x(j). (Note that the Jacobian J is the transpose of the gradient of F.)

options
Options provides the function-specific details for the options parameters.

`fun`	The function whose sum-of-squares is minimized. `fun` is a function that accepts a vector `x` and returns a vector `F`, the objective functions evaluated at `x`. The function `fun` can be specified as a function handle. x = lsqnonlin(@myfun,x0) where `myfun` is a MATLAB function such as function F = myfun(x) F = ... % Compute function values at x `fun` can also be an inline object. x = lsqnonlin(inline('sin(x.x)'),x0); If the Jacobian can also be computed and* the `Jacobian` parameter is `'on'`, set by options = optimset('Jacobian','on') then the function `fun` must return, in a second output argument, the Jacobian value `J`, a matrix, at `x`. Note that by checking the value of `nargout` the function can avoid computing `J` when `fun` is called with only one output argument (in the case where the optimization algorithm only needs the value of `F` but not `J`). function [F,J] = myfun(x) F = ... % Objective function values at x if nargout > 1 % Two output arguments J = ... % Jacobian of the function evaluated at x end If `fun` returns a vector (matrix) of `m` components and `x` has length `n`, where `n` is the length of `x0`, then the Jacobian `J` is an m-by-n matrix where `J(i,j)` is the partial derivative of `F(i)` with respect to `x(j)`. (Note that the Jacobian `J` is the transpose of the gradient of `F`.)
`options`	Options provides the function-specific details for the `options` parameters.

Output Arguments

Function Arguments contains general descriptions of arguments returned by lsqnonlin. This section provides function-specific details for exitflag, lambda, and output:

exitflag

Describes the exit condition:

> 0
The function converged to a solution x.

0
The maximum number of function evaluations or iterations was exceeded.

< 0
The function did not converge to a solution.

lambda

Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields are:

lower
Lower bounds lb

upper
Upper bounds ub

output
Structure containing information about the optimization. The fields are:

iterations
Number of iterations taken

funcCount
The number of function evaluations

algorithm
Algorithm used

cgiterations
Number of PCG iterations (large-scale algorithm only)

stepsize
The final step size taken (medium-scale algorithm only)

firstorderopt
Measure of first-order optimality (large-scale algorithm only)
For large-scale bound constrained problems, the first-order optimality is the infinity norm of v.*g, where v is defined as in Box Constraints, and g is the gradient g = J^TF (see Nonlinear Least-Squares).

`exitflag`	Describes the exit condition:
	`> 0`	The function converged to a solution `x`.
	`0`	The maximum number of function evaluations or iterations was exceeded.
	`< 0`	The function did not converge to a solution.
`lambda`	Structure containing the Lagrange multipliers at the solution `x` (separated by constraint type). The fields are:
	`lower`	Lower bounds `lb`
	`upper`	Upper bounds `ub`
`output`	Structure containing information about the optimization. The fields are:
	`iterations`	Number of iterations taken
	`funcCount`	The number of function evaluations
	`algorithm`	Algorithm used
	`cgiterations`	Number of PCG iterations (large-scale algorithm only)
	`stepsize`	The final step size taken (medium-scale algorithm only)
	`firstorderopt`	Measure of first-order optimality (large-scale algorithm only) For large-scale bound constrained problems, the first-order optimality is the infinity norm of `v.*g`, where `v` is defined as in Box Constraints, and `g` is the gradient g = J^TF (see Nonlinear Least-Squares).

Note The sum of squares should not be formed explicitly. Instead, your function should return a vector of function values. See the example below.

Options

Optimization parameter options. You can set or change the values of these parameters using the optimset function. Some parameters apply to all algorithms, some are only relevant when using the large-scale algorithm, and others are only relevant when using the medium-scale algorithm. See Optimization Parameters for detailed information.

We start by describing the LargeScale option since it states a preference for which algorithm to use. It is only a preference because certain conditions must be met to use the large-scale or medium-scale algorithm. For the large-scale algorithm, the nonlinear system of equations cannot be under-determined; that is, the number of equations (the number of elements of F returned by fun) must be at least as many as the length of x. Furthermore, only the large-scale algorithm handles bound constraints:

LargeScale
Use large-scale algorithm if possible when set to 'on'. Use medium-scale algorithm when set to 'off'.

`LargeScale`	Use large-scale algorithm if possible when set to `'on'`. Use medium-scale algorithm when set to `'off'`.

Medium-Scale and Large-Scale Algorithms. These parameters are used by both the medium-scale and large-scale algorithms:

Diagnostics
Print diagnostic information about the function to be minimized.

Display
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output.

Jacobian
If 'on', lsqnonlin uses a user-defined Jacobian (defined in fun), or Jacobian information (when using JacobMult), for the objective function. If 'off', lsqnonlin approximates the Jacobian using finite differences.

MaxFunEvals
Maximum number of function evaluations allowed.

MaxIter
Maximum number of iterations allowed.

TolFun
Termination tolerance on the function value.

TolX
Termination tolerance on x.

`Diagnostics`	Print diagnostic information about the function to be minimized.
`Display`	Level of display. `'off'` displays no output; `'iter'` displays output at each iteration; `'final'` (default) displays just the final output.
`Jacobian`	If `'on'`, `lsqnonlin` uses a user-defined Jacobian (defined in `fun`), or Jacobian information (when using `JacobMult`), for the objective function. If `'off'`, `lsqnonlin` approximates the Jacobian using finite differences.
`MaxFunEvals`	Maximum number of function evaluations allowed.
`MaxIter`	Maximum number of iterations allowed.
`TolFun`	Termination tolerance on the function value.
`TolX`	Termination tolerance on `x`.

Large-Scale Algorithm Only. These parameters are used only by the large-scale algorithm:

JacobMult
Function handle for Jacobian multiply function. For large-scale structured problems, this function computes the Jacobian matrix products J*Y, J'*Y, or J'*(J*Y) without actually forming J. The function is of the form
W = jmfun(Jinfo,Y,flag,p1,p2,...)
where Jinfo and the additional parameters p1,p2,... contain the matrices used to compute J*Y (or J'*Y, or J'*(J*Y)). The first argument Jinfo must be the same as the second argument returned by the objective function fun.
[F,Jinfo] = fun(x,p1,p2,...)
The parameters p1,p2,... are the same additional parameters that are passed to lsqnonlin (and to fun).
lsqnonlin(fun,...,options,p1,p2,...)
Y is a matrix that has the same number of rows as there are dimensions in the problem. flag determines which product to compute. If flag == 0 then W = J'*(J*Y). If flag > 0 then W = J*Y. If flag < 0 then W = J'*Y. In each case, J is not formed explicitly. lsqnonlin uses Jinfo to compute the preconditioner.
Note 'Jacobian' must be set to 'on' for Jinfo to be passed from fun to jmfun.

See Nonlinear Minimization with a Dense but Structured Hessian and Equality Constraints for a similar example.

JacobPattern
Sparsity pattern of the Jacobian for finite-differencing. If it is not convenient to compute the Jacobian matrix J in fun, lsqnonlin can approximate J via sparse finite-differences provided the structure of J, i.e., locations of the nonzeros, is supplied as the value for JacobPattern. In the worst case, if the structure is unknown, you can set JacobPattern to be a dense matrix and a full finite-difference approximation is computed in each iteration (this is the default if JacobPattern is not set). This can be very expensive for large problems so it is usually worth the effort to determine the sparsity structure.

MaxPCGIter
Maximum number of PCG (preconditioned conjugate gradient) iterations (see the Algorithm section below).

PrecondBandWidth
Upper bandwidth of preconditioner for PCG. By default, diagonal preconditioning is used (upper bandwidth of 0). For some problems, increasing the bandwidth reduces the number of PCG iterations.

TolPCG
Termination tolerance on the PCG iteration.

TypicalX
Typical x values.

Medium-Scale Algorithm Only. These parameters are used only by the medium-scale algorithm:

DerivativeCheck
Compare user-supplied derivatives (Jacobian) to finite-differencing derivatives.

DiffMaxChange
Maximum change in variables for finite-differencing.

DiffMinChange
Minimum change in variables for finite-differencing.

LevenbergMarquardt
Choose Levenberg-Marquardt over Gauss-Newton algorithm.

LineSearchType
Line search algorithm choice.

`DerivativeCheck`	Compare user-supplied derivatives (Jacobian) to finite-differencing derivatives.
`DiffMaxChange`	Maximum change in variables for finite-differencing.
`DiffMinChange`	Minimum change in variables for finite-differencing.
`LevenbergMarquardt`	Choose Levenberg-Marquardt over Gauss-Newton algorithm.
`LineSearchType`	Line search algorithm choice.

Examples

Find x that minimizes

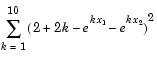
starting at the point x = [0.3, 0.4].

Because lsqnonlin assumes that the sum-of-squares is not explicitly formed in the user function, the function passed to lsqnonlin should instead compute the vector valued function

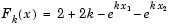
for 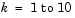(that is, F should have k components).

First, write an M-file to compute the k-component vector F.

function F = myfun(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));

Next, invoke an optimization routine.

x0 = [0.3 0.4]                        % Starting guess
[x,resnorm] = lsqnonlin(@myfun,x0)    % Invoke optimizer

After about 24 function evaluations, this example gives the solution

x = 
     0.2578   0.2578
resnorm       % Residual or sum of squares
resnorm = 
     124.3622

Algorithm

Large-Scale Optimization. By default lsqnonlin chooses the large-scale algorithm. This algorithm is a subspace trust region method and is based on the interior-reflective Newton method described in [1], [2]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG). See Trust-Region Methods for Nonlinear Minimization and Preconditioned Conjugate Gradients.

Medium-Scale Optimization. lsqnonlin, with the LargeScale parameter set to 'off' with optimset, uses the Levenberg-Marquardt method with line-search [4], [5], [6]. Alternatively, a Gauss-Newton method [3] with line-search may be selected. The choice of algorithm is made by setting the LevenbergMarquardt parameter. Setting LevenbergMarquardt to 'off' (and LargeScale to 'off') selects the Gauss-Newton method, which is generally faster when the residual 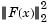is small.

The default line search algorithm, i.e., the LineSearchType parameter set to 'quadcubic', is a safeguarded mixed quadratic and cubic polynomial interpolation and extrapolation method. A safeguarded cubic polynomial method can be selected by setting the LineSearchType parameter to 'cubicpoly'. This method generally requires fewer function evaluations but more gradient evaluations. Thus, if gradients are being supplied and can be calculated inexpensively, the cubic polynomial line search method is preferable. The algorithms used are described fully in the Standard Algorithms chapter.

Diagnostics

Large-Scale Optimization. The large-scale code does not allow equal upper and lower bounds. For example if lb(2)==ub(2) then lsqlin gives the error

Equal upper and lower bounds not permitted.

(lsqnonlin does not handle equality constraints, which is another way to formulate equal bounds. If equality constraints are present, use fmincon, fminimax or fgoalattain for alternative formulations where equality constraints can be included.)

Limitations

The function to be minimized must be continuous. lsqnonlin may only give local solutions.

lsqnonlin only handles real variables. When x has complex variables, the variables must be split into real and imaginary parts.

Large-Scale Optimization. The large-scale method for lsqnonlin does not solve under-determined systems; it requires that the number of equations (i.e., the number of elements of F) be at least as great as the number of variables. In the under-determined case, the medium-scale algorithm is used instead. (If bound constraints exist, a warning is issued and the problem is solved with the bounds ignored.) See Table 2-4, Large-Scale Problem Coverage and Requirements,, for more information on what problem formulations are covered and what information must be provided.

The preconditioner computation used in the preconditioned conjugate gradient part of the large-scale method forms J^TJ (where J is the Jacobian matrix) before computing the preconditioner; therefore, a row of J with many nonzeros, which results in a nearly dense product J^TJ, may lead to a costly solution process for large problems.

If components of x have no upper (or lower) bounds, then lsqnonlin prefers that the corresponding components of ub (or lb) be set to inf (or -inf for lower bounds) as opposed to an arbitrary but very large positive (or negative for lower bounds) number.

Currently, if the analytical Jacobian is provided in fun, the options parameter DerivativeCheck cannot be used with the large-scale method to compare the analytic Jacobian to the finite-difference Jacobian. Instead, use the medium-scale method to check the derivatives with options parameter MaxIter set to 0 iterations. Then run the problem with the large-scale method.

Medium-Scale Optimization. The medium-scale algorithm does not handle bound constraints.

Since the large-scale algorithm does not handle under-determined systems and the medium-scale does not handle bound constraints, problems with both these characteristics cannot be solved by lsqnonlin.

See Also

@ (function_handle), lsqcurvefit, lsqlin, optimset

References

[1] Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.

[2] Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.

[3] Dennis, J.E., Jr., "Nonlinear Least-Squares," State of the Art in Numerical Analysis, ed. D. Jacobs, Academic Press, pp. 269-312, 1977.

[4] Levenberg, K.,"A Method for the Solution of Certain Problems in Least-Squares," Quarterly Applied Math. 2, pp. 164-168, 1944.

[5] Marquardt, D.,"An Algorithm for Least-Squares Estimation of Nonlinear Parameters," SIAM Journal Applied Math. Vol. 11, pp. 431-441, 1963.

[6] Moré, J.J., "The Levenberg-Marquardt Algorithm: Implementation and Theory," Numerical Analysis, ed. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, pp. 105-116, 1977.

lsqlin lsqnonneg