Optimization Toolbox

Box Constraints

The box constrained problem is of the form

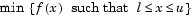
(4-7)

where l is a vector of lower bounds, and u is a vector of upper bounds. Some (or all) of the components of 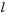can be equal to 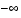and some (or all) of the components of 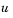can be equal to 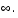The method generates a sequence of strictly feasible points. Two techniques are used to maintain feasibility while achieving robust convergence behavior. First, a scaled modified Newton step replaces the unconstrained Newton step (to define the two-dimensional subspace 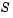). Second, reflections are used to increase the stepsize.

The scaled modified Newton step arises from examining the Kuhn-Tucker necessary conditions for Eq. 4-7,

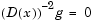
(4-8)

where

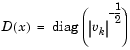
and the vector 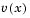is defined below, for each :

• If and then
• If and then
• If and then
• If and then

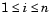The nonlinear system Eq. 4-8 is not differentiable everywhere. Nondifferentiability occurs when 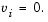You can avoid such points by maintaining strict feasibility, i.e., restricting .

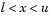The scaled modified Newton step 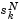for Eq. 4-8 is defined as the solution to the linear system

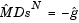
(4-9)

where

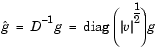
(4-10)

and

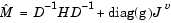
(4-11)

Here 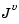plays the role of the Jacobian of 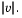Each diagonal component of the diagonal matrix 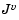equals 0, -1, or 1. If all the components of l and u are finite, 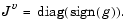At a point where 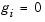, 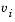might not be differentiable. 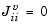is defined at such a point. Nondifferentiability of this type is not a cause for concern because, for such a component, it is not significant which value 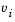takes. Further, 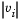will still be discontinuous at this point, but the function 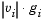is continuous.

Second, reflections are used to increase the stepsize. A (single) reflection step is defined as follows. Given a step 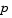that intersects a bound constraint, consider the first bound constraint crossed by p; assume it is the ith bound constraint (either the ith upper or ith lower bound). Then the reflection step 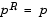except in the ith component, where .

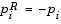Linear Equality Constraints

Nonlinear Least-Squares