| Optimization Toolbox | |
Linear Equality Constraints
The general linear equality constrained minimization problem can be written
|
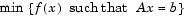
(4-5) |
where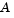 
is an m-by-n matrix (
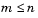). The Optimization Toolbox preprocesses 
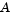to remove strict linear dependencies using a technique based on the LU-factorization of 
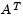[6]. Here 
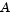is assumed to be of rank m.
The method used to solve Eq. 4-5 differs from the unconstrained approach in two significant ways. First, an initial feasible point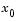 
is computed, using a sparse least-squares step, so that 
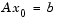. Second, Algorithm PCG is replaced with Reduced Preconditioned Conjugate Gradients (RPCG), see [6], in order to compute an approximate reduced Newton step (or a direction of negative curvature in the null space of 
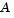). The key linear algebra step involves solving systems of the form
|
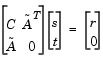
(4-6) |
where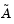 
approximates 
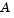(small nonzeros of 
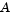are set to zero provided rank is not lost) and 
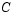is a sparse symmetric positive-definite approximation to H, i.e., 
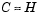. See [6] for more details.
| | Linearly Constrained Problems | Box Constraints | |