Optimization Toolbox

lsqnonneg

Solves the nonnegative least-squares problem

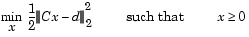
where the matrix C and the vector d are the coefficients of the objective function. The vector, x, of independent variables is restricted to be nonnegative.

Syntax

• x = lsqnonneg(C,d)
  x = lsqnonneg(C,d,x0)
  x = lsqnonneg(C,d,x0,options)
  [x,resnorm] = lsqnonneg(...)
  [x,resnorm,residual] = lsqnonneg(...)
  [x,resnorm,residual,exitflag] = lsqnonneg(...)
  [x,resnorm,residual,exitflag,output] = lsqnonneg(...)
  [x,resnorm,residual,exitflag,output,lambda] = lsqnonneg(...)
  

Description

x = lsqnonneg(C,d) returns the vector x that minimizes norm(C*x-d) subject to x >= 0. C and d must be real.

x = lsqnonneg(C,d,x0) uses x0 as the starting point if all x0 >= 0; otherwise, the default is used. The default start point is the origin (the default is also used when x0==[] or when only two input arguments are provided).

x = lsqnonneg(C,d,x0,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

[x,resnorm] = lsqnonneg(...) returns the value of the squared 2-norm of the residual, norm(C*x-d)^2.

[x,resnorm,residual] = lsqnonneg(...) returns the residual, C*x-d.

[x,resnorm,residual,exitflag] = lsqnonneg(...) returns a value exitflag that describes the exit condition of lsqnonneg.

[x,resnorm,residual,exitflag,output] = lsqnonneg(...) returns a structure output that contains information about the optimization.

[x,resnorm,residual,exitflag,output,lambda] = lsqnonneg(...) returns the Lagrange multipliers in the vector lambda.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to lsqnonneg. This section provides function-specific details for options:

options	Use optimset to set or change the values of these fields in the parameters structure, options. See Table 5, Optimization Parameters,, for detailed information.
	Display	Level of display. 'off' displays no output; 'final' displays just the final output; 'notify' (default) dislays output only if the function does not converge.
	TolX	Termination tolerance on x.

Output Arguments

Function Arguments contains general descriptions of arguments returned by lsqnonneg. This section provides function-specific details for exitflag, lambda, and output:

exitflag	Describes the exit condition:
	> 0	The function converged to a solution x.
	0	The maximum number of function evaluations or iterations was exceeded. Increasing the tolerance TolX may lead to a solution.
lambda	Vector containing the Lagrange multipliers: lambda(i)<=0 when x(i) is (approximately) 0, and lambda(i) is (approximately) 0 when x(i)>0.
output	Structure containing information about the optimization. The fields are:
	iterations	Number of iterations taken
	algorithm	Algorithm used

Examples

Compare the unconstrained least-squares solution to the lsqnonneg solution for a 4-by-2 problem.

• C = [
       0.0372    0.2869
       0.6861    0.7071
       0.6233    0.6245
       0.6344    0.6170];
  d = [
       0.8587
       0.1781
       0.0747
       0.8405];
  
  [C\d, lsqnonneg(C,d)] =
      -2.5627    0
       3.1108    0.6929
  
  [norm(C*(C\d)-d), norm(C*lsqnonneg(C,d)-d)] =
          0.6674 0.9118
  

The solution from lsqnonneg does not fit as well as the least-squares solution. However, the nonnegative least-squares solution has no negative components.

Algorithm

lsqnonneg uses the algorithm described in [1]. The algorithm starts with a set of possible basis vectors and computes the associated dual vector lambda. It then selects the basis vector corresponding to the maximum value in lambda in order to swap it out of the basis in exchange for another possible candidate. This continues until lambda <= 0.

Notes

The nonnegative least-squares problem is a subset of the constrained linear least-squares problem. Thus, when C has more rows than columns (i.e., the system is over-determined)

• [x,resnorm,residual,exitflag,output,lambda] = lsqnonneg(C,d)
  

is equivalent to

• [m,n] = size(C);
  [x,resnorm,residual,exitflag,output,lambda_lsqlin] = 
     lsqlin(C,d,-eye(n,n),zeros(n,1));
  

except that lambda = -lambda_lsqlin.ineqlin.

For problems greater than order 20, lsqlin may be faster than lsqnonneg, otherwise lsqnonneg is generally more efficient.

See Also

\, lsqlin, optimset

References

[1]  Lawson, C.L. and R.J. Hanson, Solving Least-Squares Problems, Prentice-Hall, Chapter 23, p. 161, 1974.

lsqnonlin

optimget