

| MATLAB Function Reference |   |
Syntax
Description
MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element-by-element, and can be used with multidimensional arrays. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs .+ and .- are not used.
Addition or unary plus. A+B adds A and B. A and B must have the same size, unless one is a scalar. A scalar can be added to a matrix of any size. |
|
Subtraction or unary minus. A-B subtracts B from A. A and B must have the same size, unless one is a scalar. A scalar can be subtracted from a matrix of any size. |
|
Matrix multiplication. C = A*B is the linear algebraic product of the matrices A and B. More precisely,For nonscalar A and B, the number of columns of A must equal the number of rows of B. A scalar can multiply a matrix of any size. |
|
Array multiplication. A.*B is the element-by-element product of the arrays A and B. A and B must have the same size, unless one of them is a scalar. |
|
Slash or matrix right division. B/A is roughly the same as B*inv(A). More precisely, B/A = (A'\B')'. See \. |
|
Array right division. A./B is the matrix with elements A(i,j)/B(i,j). A and B must have the same size, unless one of them is a scalar. |
|
Backslash or matrix left division. If A is a square matrix, A\B is roughly the same as inv(A)*B, except it is computed in a different way. If A is an n-by-n matrix and B is a column vector with n components, or a matrix with several such columns, then X = A\B is the solution to the equation AX = B computed by Gaussian elimination (see Algorithm for details). A warning message prints if A is badly scaled or nearly singular. |
|
If A is an m-by-n matrix with m ~= n and B is a column vector with m components, or a matrix with several such columns, then X = A\B is the solution in the least squares sense to the under- or overdetermined system of equations AX = B. The effective rank, k, of A, is determined from the QR decomposition with pivoting (see "Algorithm" for details). A solution X is computed which has at most k nonzero components per column. If k < n, this is usually not the same solution as pinv(A)*B, which is the least squares solution with the smallest norm, 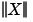 . . |
|
Array left division. A.\B is the matrix with elements B(i,j)/A(i,j). A and B must have the same size, unless one of them is a scalar. |
|
Matrix power. X^p is X to the power p, if p is a scalar. If p is an integer, the power is computed by repeated squaring. If the integer is negative, X is inverted first. For other values of p, the calculation involves eigenvalues and eigenvectors, such that if [V,D] = eig(X), then X^p = V*D.^p/V. |
|
If x is a scalar and P is a matrix, x^P is x raised to the matrix power P using eigenvalues and eigenvectors. X^P, where X and P are both matrices, is an error. |
|
Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar. |
|
Matrix transpose. A' is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose. |
|
Array transpose. A.' is the array transpose of A. For complex matrices, this does not involve conjugation. |
Remarks
The arithmetic operators have M-file function equivalents, as shown:
Examples
Here are two vectors, and the results of various matrix and array operations on them, printed with format rat.
Algorithm
The specific algorithm used for solving the simultaneous linear equations denoted by X = A\B and X = B/A depends upon the structure of the coefficient matrix A. To determine the structure of A and select the appropriate algorithm, MATLAB follows this precedence:
1.0 if there are no zeros on any of the three diagonals.
A is real and tridiagonal, i.e., band density = 1.0, and B is real with only one column, X is computed quickly using Gaussian elimination without pivoting.
A or B is not real, or if B has more than one column, but A is banded with band density greater than the spparms parameter 'bandden' (default = 0.5), then X is computed using LAPACK.
X is computed quickly with a backsubstitution algorithm for upper triangular matrices, or a forward substitution algorithm for lower triangular martrices. The check for triangularity is done for full matrices by testing for zero elements and for sparse matrices by accessing the sparse data structure.
X is computed with a permuted backsubstitution algorithm.
chol). If A is found to be positive definite, the Cholesky factorization attempt is successful and requires less than half the time of a general factorization. Nonpositive definite matrices are usually detected almost immediately, so this check also requires little time. If successful, the Cholesky factorization is
R is upper triangular. The solution X is computed by solving two triangular systems,
If A is sparse, a symmetric minimum degree preordering is applied (see symmmd and spparms). The algorithm is:
lu). This results in
L is a permutation of a lower triangular matrix and U is an upper triangular matrix. Then X is computed by solving two permuted triangular systems.
If A is sparse, then UMFPACK is used to compute X. The computations result in
where P is a row permutaion matrix and Q is a column reordering matrix. Then X = Q*(U\L\(P*B)).
P is a permutation, Q is orthogonal and R is upper triangular (see qr). The least squares solution X is computed with
If A is sparse, then MATLAB computes a least squares solution using the sparse qr factorization of A.
Note
For sparse matrices, to see information about choice of algorithm and storage allocation, set the spparms parameter 'spumoni' = 1.
|
MATLAB uses LAPACK routines to compute these matrix factorizations:
Diagnostics
A is singular:
A is rank deficient:
See Also
chol, det, inv, lu, orth, permute, ipermute, qr, rref
References
[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide (http://www.netlib.org/lapack/lug/lapack_lug.html), Third Edition, SIAM, Philadelphia, 1999.
[2] Davis, T.A., UMFPACK Version 4.0 User Guide (http://www.cise.ufl.edu/research/sparse/umfpack/v4.0/UserGuide.pdf), Dept. of Computer and Information Science and Engineering, Univ. of Florida, Gainesville, FL, 2002.
 | wait | Relational Operators < > <= >= == ~= |  |