

| Optimization Toolbox |   |
Preconditioned Conjugate Gradients
A popular way to solve large symmetric positive definite systems of linear equations 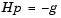 is the method of Preconditioned Conjugate Gradients (PCG). This iterative approach requires the ability to calculate matrix-vector products of the form
is the method of Preconditioned Conjugate Gradients (PCG). This iterative approach requires the ability to calculate matrix-vector products of the form 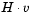 where
where 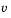 is an arbitrary vector. The symmetric positive definite matrix M is a preconditioner for H. That is,
is an arbitrary vector. The symmetric positive definite matrix M is a preconditioner for H. That is, 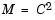 where
where 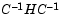 is a well-conditioned matrix or a matrix with clustered eigenvalues.
is a well-conditioned matrix or a matrix with clustered eigenvalues.
Algorithm
The Optimization Toolbox uses this PCG algorithm, which it refers to as Algorithm PCG.
% Initializations r = -g; p = zeros(n,1); % Precondition z = M\r; inner1 = r'*z; inner2 = 0; d = z; % Conjugate gradient iteration for k = 1:kmax if k > 1 beta = inner1/inner2; d = z + beta*d; end w = H*d; denom = d'*w; if denom <= 0 p = d/norm(d); % Direction of negative/zero curvature break % Exit if zero/negative curvature detected else alpha = inner1/denom; p = p + alpha*d; r = r - alpha*w; end z = M\r; if norm(z) <= tol % Exit if Hp=-g solved within tolerance break end inner2 = inner1; inner1 = r'*z; end
In a minimization context, you can assume that the Hessian matrix 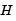 is symmetric. However,
is symmetric. However, 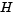 is guaranteed to be positive definite only in the neighborhood of a strong minimizer. Algorithm PCG exits when a direction of negative (or zero) curvature is encountered, i.e.,
is guaranteed to be positive definite only in the neighborhood of a strong minimizer. Algorithm PCG exits when a direction of negative (or zero) curvature is encountered, i.e., 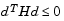 . The PCG output direction, p, is either a direction of negative curvature or an approximate (tol controls how approximate) solution to the Newton system
. The PCG output direction, p, is either a direction of negative curvature or an approximate (tol controls how approximate) solution to the Newton system 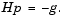 In either case
In either case  is used to help define the two-dimensional subspace used in the trust-region approach discussed in Trust-Region Methods for Nonlinear Minimization.
is used to help define the two-dimensional subspace used in the trust-region approach discussed in Trust-Region Methods for Nonlinear Minimization.
 | Trust-Region Methods for Nonlinear Minimization | Linearly Constrained Problems |  |