

| Optimization Toolbox |   |
Find a minimum of a constrained nonlinear multivariable function
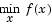 subject to
subject to
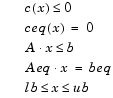
where x, b, beq, lb, and ub are vectors, A and Aeq are matrices, c(x) and ceq(x) are functions that return vectors, and f(x) is a function that returns a scalar. f(x), c(x), and ceq(x) can be nonlinear functions.
Syntax
x = fmincon(fun,x0,A,b) x = fmincon(fun,x0,A,b,Aeq,beq) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2, ...) [x,fval] = fmincon(...) [x,fval,exitflag] = fmincon(...) [x,fval,exitflag,output] = fmincon(...) [x,fval,exitflag,output,lambda] = fmincon(...) [x,fval,exitflag,output,lambda,grad] = fmincon(...) [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(...)
Description
fmincon finds a constrained minimum of a scalar function of several variables starting at an initial estimate. This is generally referred to as constrained nonlinear optimization or nonlinear programming.
x = fmincon(fun,x0,A,b)
starts at x0 and finds a minimum x to the function described in fun subject to the linear inequalities A*x <= b. x0 can be a scalar, vector, or matrix.
x = fmincon(fun,x0,A,b,Aeq,beq)
minimizes fun subject to the linear equalities Aeq*x = beq as well as A*x <= b. Set A=[] and b=[] if no inequalities exist.
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
defines a set of lower and upper bounds on the design variables, x, so that the solution is always in the range lb <= x <= ub. Set Aeq=[] and beq=[] if no equalities exist.
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
subjects the minimization to the nonlinear inequalities c(x) or equalities ceq(x) defined in nonlcon. fmincon optimizes such that c(x) <= 0 and ceq(x) = 0. Set lb=[] and/or ub=[] if no bounds exist.
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2,...)
passes the problem-dependent parameters P1, P2, etc., directly to the functions fun and nonlcon. Pass empty matrices as placeholders for A, b, Aeq, beq, lb, ub, nonlcon, and options if these arguments are not needed.
[x,fval] = fmincon(...)
returns the value of the objective function fun at the solution x.
[x,fval,exitflag] = fmincon(...)
returns a value exitflag that describes the exit condition of fmincon.
[x,fval,exitflag,output] = fmincon(...)
returns a structure output with information about the optimization.
[x,fval,exitflag,output,lambda] = fmincon(...)
returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.
[x,fval,exitflag,output,lambda,grad] = fmincon(...)
returns the value of the gradient of fun at the solution x.
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(...)
returns the value of the Hessian of fun at the solution x.
Input Arguments
Function Arguments contains general descriptions of arguments passed in to fmincon. This "Arguments" section provides function-specific details for fun, nonlcon, and options:
fun |
The function to be minimized. fun is a function that accepts a scalar x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle.where myfun is a MATLAB function such asfun can also be an inline object.If the gradient of fun can also be computed and the GradObj parameter is 'on', as set bythen the function fun must return, in the second output argument, the gradient value g, a vector, at x. Note that by checking the value of nargout the function can avoid computing g when fun is called with only one output argument (in the case where the optimization algorithm only needs the value of f but not g).
f at the point x. That is, the ith component of g is the partial derivative of f with respect to the ith component of x.If the Hessian matrix can also be computed and the Hessian parameter is 'on', i.e., options = optimset('Hessian','on'), then the function fun must return the Hessian value H, a symmetric matrix, at x in a third output argument. Note that by checking the value of nargout we can avoid computing H when fun is called with only one or two output arguments (in the case where the optimization algorithm only needs the values of f and g but not H). |
f at the point x. That is, the (i,j)th component of H is the second partial derivative of f with respect to xi and xj, 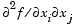 . The Hessian is by definition a symmetric matrix. . The Hessian is by definition a symmetric matrix. |
|
nonlcon |
The function that computes the nonlinear inequality constraints c(x)<= 0 and the nonlinear equality constraints ceq(x) = 0. The function nonlcon accepts a vector x and returns two vectors c and ceq. The vector c contains the nonlinear inequalities evaluated at x, and ceq contains the nonlinear equalities evaluated at x. The function nonlcon can be specified as a function handle.where mycon is a MATLAB function such as
If the gradients of the constraints can also be computed and the nonlcon must also return, in the third and fourth output arguments, GC, the gradient of c(x), and GCeq, the gradient of ceq(x). Note that by checking the value of nargout the function can avoid computing GC and GCeq when nonlcon is called with only two output arguments (in the case where the optimization algorithm only needs the values of c and ceq but not GC and GCeq). |
nonlcon returns a vector c of m components and x has length n, where n is the length of x0, then the gradient GC of c(x) is an n-by-m matrix, where GC(i,j) is the partial derivative of c(j) with respect to x(i) (i.e., the jth column of GC is the gradient of the jth inequality constraint c(j)). Likewise, if ceq has p components, the gradient GCeq of ceq(x) is an n-by-p matrix, where GCeq(i,j) is the partial derivative of ceq(j) with respect to x(i) (i.e., the jth column of GCeq is the gradient of the jth equality constraint ceq(j)). |
|
options |
Options provides the function-specific details for the options parameters. |
Output Arguments
Function Arguments contains general descriptions of arguments returned by fmincon. This section provides function-specific details for exitflag, lambda, and output:
exitflag |
Describes the exit condition: | |
| > 0 |
The function converged to a solution x. |
|
| 0 |
The maximum number of function evaluations or iterations was exceeded. |
|
| < 0 |
The function did not converge to a solution. |
|
lambda |
Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields of the structure are: | |
lower |
Lower bounds lb |
|
upper |
Upper bounds ub |
|
ineqlin |
Linear inequalities |
|
eqlin |
Linear equalities |
|
ineqnonlin |
Nonlinear inequalities |
|
eqnonlin |
Nonlinear equalities |
|
output |
Structure containing information about the optimization. The fields of the structure are: | |
iterations |
Number of iterations taken. |
|
funcCount |
Number of function evaluations. |
|
algorithm |
Algorithm used. |
|
cgiterations |
Number of PCG iterations (large-scale algorithm only). |
|
stepsize |
Final step size taken (medium-scale algorithm only). |
|
firstorderopt |
Measure of first-order optimality (large-scale algorithm only). For large-scale bound constrained problems, the first-order optimality is the infinity norm of v.*g, where v is defined as in Box Constraints, and g is the gradient.For large-scale problems with only linear equalities, the first-order optimality is the infinity norm of the projected gradient (i.e. the gradient projected onto the nullspace of Aeq). |
|
Options
Optimization options parameters used by fmincon. Some parameters apply to all algorithms, some are only relevant when using the large-scale algorithm, and others are only relevant when using the medium-scale algorithm.You can use optimset to set or change the values of these fields in the parameters structure, options. See Optimization Parameters, for detailed information.
We start by describing the LargeScale option since it states a preference for which algorithm to use. It is only a preference since certain conditions must be met to use the large-scale algorithm. For fmincon, you must provide the gradient (see the description of fun above to see how) or else the medium-scale algorithm is used:
LargeScale |
Use large-scale algorithm if possible when set to 'on'. Use medium-scale algorithm when set to 'off'. |
Medium-Scale and Large-Scale Algorithms. These parameters are used by both the medium-scale and large-scale algorithms:
Diagnostics |
Print diagnostic information about the function to be minimized. |
Display |
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output. |
GradObj |
Gradient for the objective function defined by user. See the description of fun above to see how to define the gradient in fun. You must provide the gradient to use the large-scale method. It is optional for the medium-scale method. |
MaxFunEvals |
Maximum number of function evaluations allowed. |
MaxIter |
Maximum number of iterations allowed. |
TolFun |
Termination tolerance on the function value. |
TolCon |
Termination tolerance on the constraint violation. |
TolX |
Termination tolerance on x. |
Large-Scale Algorithm Only. These parameters are used only by the large-scale algorithm:
Hessian |
If 'on', fmincon uses a user-defined Hessian (defined in fun), or Hessian information (when using HessMult), for the objective function. If 'off', fmincon approximates the Hessian using finite differences. |
HessMult |
Function handle for Hessian multiply function. For large-scale structured problems, this function computes the Hessian matrix product H*Y without actually forming H. The function is of the form |
|
where Hinfo and the additional parameters p1,p2,... contain the matrices used to compute H*Y. The first argument must be the same as the third argument returned by the objective function fun.[f,g,Hinfo] = fun(x,p1,p2,...) The parameters p1,p2,... are the same additional parameters that are passed to fmincon (and to fun).Y is a matrix that has the same number of rows as there are dimensions in the problem. W = H*Y although H is not formed explicitly. fmincon uses Hinfo to compute the preconditioner.See Nonlinear Minimization with a Dense but Structured Hessian and Equality Constraints for an example. |
HessPattern |
Sparsity pattern of the Hessian for finite-differencing. If it is not convenient to compute the sparse Hessian matrix H in fun, the large-scale method in fmincon can approximate H via sparse finite-differences (of the gradient) provided the sparsity structure of H -- i.e., locations of the nonzeros -- is supplied as the value for HessPattern. In the worst case, if the structure is unknown, you can set HessPattern to be a dense matrix and a full finite-difference approximation is computed at each iteration (this is the default). This can be very expensive for large problems so it is usually worth the effort to determine the sparsity structure. |
MaxPCGIter |
Maximum number of PCG (preconditioned conjugate gradient) iterations (see the Algorithm section below). |
PrecondBandWidth |
Upper bandwidth of preconditioner for PCG. By default, diagonal preconditioning is used (upper bandwidth of 0). For some problems, increasing the bandwidth reduces the number of PCG iterations. |
TolPCG |
Termination tolerance on the PCG iteration. |
TypicalX |
Typical x values. |
Medium-Scale Algorithm Only. These parameters are used only by the medium-scale algorithm:
Examples
Find values of x that minimize 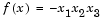 , starting at the point
, starting at the point x = [10; 10; 10] and subject to the constraints
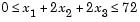
First, write an M-file that returns a scalar value f of the function evaluated at x.
Then rewrite the constraints as both less than or equal to a constant,
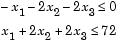
Since both constraints are linear, formulate them as the matrix inequality 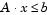 where
where
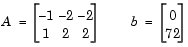
Next, supply a starting point and invoke an optimization routine.
After 66 function evaluations, the solution is
and linear inequality constraints evaluate to be <= 0
Notes
Large-Scale Optimization. To use the large-scale method, the gradient must be provided in fun (and the GradObj parameter is set to 'on'). A warning is given if no gradient is provided and the LargeScale parameter is not 'off'. The function fmincon permits g(x) to be an approximate gradient but this option is not recommended; the numerical behavior of most optimization codes is considerably more robust when the true gradient is used.
The large-scale method in fmincon is most effective when the matrix of second derivatives, i.e., the Hessian matrix H(x), is also computed. However, evaluation of the true Hessian matrix is not required. For example, if you can supply the Hessian sparsity structure (using the HessPattern parameter in options), then fmincon computes a sparse finite-difference approximation to H(x).
If x0 is not strictly feasible, fmincon chooses a new strictly feasible (centered) starting point.
If components of x have no upper (or lower) bounds, then fmincon prefers that the corresponding components of ub (or lb) be set to Inf (or -Inf for lb) as opposed to an arbitrary but very large positive (or negative in the case of lower bounds) number.
Several aspects of linearly constrained minimization should be noted:
Aeq can result in considerable fill and computational cost.
fmincon removes (numerically) linearly dependent rows in Aeq; however, this process involves repeated matrix factorizations and therefore can be costly if there are many dependencies.
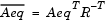
where RT is the Cholesky factor of the preconditioner. Therefore, there is a potential conflict between choosing an effective preconditioner and minimizing fill in 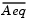 .
.
Medium-Scale Optimization. Better numerical results are likely if you specify equalities explicitly using Aeq and beq, instead of implicitly using lb and ub.
If equality constraints are present and dependent equalities are detected and removed in the quadratic subproblem, 'dependent' is printed under the Procedures heading (when you ask for output by setting the Display parameter to'iter'). The dependent equalities are only removed when the equalities are consistent. If the system of equalities is not consistent, the subproblem is infeasible and 'infeasible' is printed under the Procedures heading.
Algorithm
Large-Scale Optimization. By default fmincon will choose the large-scale algorithm if the user supplies the gradient in fun (and GradObj is 'on' in options) and if only upper and lower bounds exist or only linear equality constraints exist. This algorithm is a subspace trust region method and is based on the interior-reflective Newton method described in [1], [2]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG). See the trust-region and preconditioned conjugate gradient method descriptions in the Large-Scale Algorithms chapter.
Medium-Scale Optimization. fmincon uses a Sequential Quadratic Programming (SQP) method. In this method, a Quadratic Programming (QP) subproblem is solved at each iteration. An estimate of the Hessian of the Lagrangian is updated at each iteration using the BFGS formula (see fminunc, references [7], [8]).
A line search is performed using a merit function similar to that proposed by [4], [5], and [6]. The QP subproblem is solved using an active set strategy similar to that described in [3]. A full description of this algorithm is found in Constrained Optimization in "Introduction to Algorithms."
See also SQP Implementation in "Introduction to Algorithms" for more details on the algorithm used.
Diagnostics
Large-Scale Optimization. The large-scale code does not allow equal upper and lower bounds. For example if lb(2)==ub(2), then fmincon gives the error
Equal upper and lower bounds not permitted in this large-scale method. Use equality constraints and the medium-scale method instead.
If you only have equality constraints you can still use the large-scale method. But if you have both equalities and bounds, you must use the medium-scale method.
Limitations
The function to be minimized and the constraints must both be continuous. fmincon may only give local solutions.
When the problem is infeasible, fmincon attempts to minimize the maximum constraint value.
The objective function and constraint function must be real-valued, that is they cannot return complex values.
Large-Scale Optimization. To use the large-scale algorithm, the user must supply the gradient in fun (and GradObj must be set 'on' in options) , and only upper and lower bounds constraints may be specified, or only linear equality constraints must exist and Aeq cannot have more rows than columns. Aeq is typically sparse. See Table 2-4, Large-Scale Problem Coverage and Requirements,, for more information on what problem formulations are covered and what information must be provided.
Currently, if the analytical gradient is provided in fun, the options parameter DerivativeCheck cannot be used with the large-scale method to compare the analytic gradient to the finite-difference gradient. Instead, use the medium-scale method to check the derivative with options parameter MaxIter set to 0 iterations. Then run the problem with the large-scale method.
See Also
@ (function_handle), fminbnd, fminsearch, fminunc, optimset
References
[1] Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.
[2] Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.
[3] Gill, P.E., W. Murray, and M.H. Wright, Practical Optimization, Academic Press, London, 1981.
[4] Han, S.P., "A Globally Convergent Method for Nonlinear Programming," Journal of Optimization Theory and Applications, Vol. 22, p. 297, 1977.
[5] Powell, M.J.D., "A Fast Algorithm for Nonlineary Constrained Optimization Calculations," Numerical Analysis, ed. G.A. Watson, Lecture Notes in Mathematics, Springer Verlag, Vol. 630, 1978.
[6] Powell, M.J.D., "The Convergence of Variable Metric Methods For Nonlinearly Constrained Optimization Calculations," Nonlinear Programming 3, (O.L. Mangasarian, R.R. Meyer, and S.M. Robinson, eds.) Academic Press, 1978.
 | fminbnd | fminimax |  |