

| Optimization Toolbox |   |
SQP Implementation
The SQP implementation consists of three main stages, which are discussed briefly in the following subsections:
Updating the Hessian Matrix
At each major iteration a positive definite quasi-Newton approximation of the Hessian of the Lagrangian function, H, is calculated using the BFGS method, where 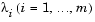 is an estimate of the Lagrange multipliers.
is an estimate of the Lagrange multipliers.
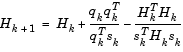 where where
|
(3-30) |
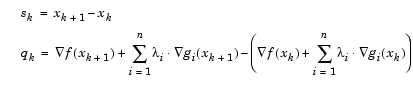
Powell [35] recommends keeping the Hessian positive definite even though it might be positive indefinite at the solution point. A positive definite Hessian is maintained providing 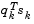 is positive at each update and that H is initialized with a positive definite matrix. When
is positive at each update and that H is initialized with a positive definite matrix. When 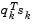 is not positive,
is not positive, 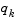 is modified on an element-by-element basis so that
is modified on an element-by-element basis so that 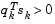 . The general aim of this modification is to distort the elements of
. The general aim of this modification is to distort the elements of 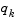 , which contribute to a positive definite update, as little as possible. Therefore, in the initial phase of the modification, the most negative element of
, which contribute to a positive definite update, as little as possible. Therefore, in the initial phase of the modification, the most negative element of 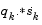 is repeatedly halved. This procedure is continued until
is repeatedly halved. This procedure is continued until 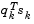 is greater than or equal to 1e-5. If, after this procedure,
is greater than or equal to 1e-5. If, after this procedure, 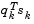 is still not positive, modify
is still not positive, modify 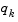 by adding a vector v multiplied by a constant scalar w, that is,
by adding a vector v multiplied by a constant scalar w, that is,
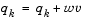
|
(3-31) |
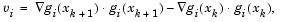
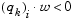 and
and 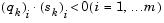
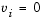 otherwise
otherwise
and increase w systematically until 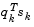 becomes positive.
becomes positive.
The functions fmincon, fminimax, fgoalattain, and fseminf all use SQP. If the options parameter Display is set to 'iter', then various information is given such as function values and the maximum constraint violation. When the Hessian has to be modified using the first phase of the preceding procedure to keep it positive definite, then Hessian modified is displayed. If the Hessian has to be modified again using the second phase of the approach described above, then Hessian modified twice is displayed. When the QP subproblem is infeasible, then infeasible is displayed. Such displays are usually not a cause for concern but indicate that the problem is highly nonlinear and that convergence might take longer than usual. Sometimes the message no update is displayed, indicating that 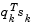 is nearly zero. This can be an indication that the problem setup is wrong or you are trying to minimize a noncontinuous function.
is nearly zero. This can be an indication that the problem setup is wrong or you are trying to minimize a noncontinuous function.
Quadratic Programming Solution
At each major iteration of the SQP method, a QP problem of the following form is solved, where 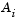 refers to the
refers to the ith row of the m-by-n matrix 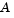 .
.
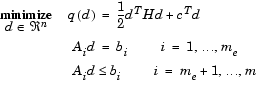
|
(3-32) |
The method used in the Optimization Toolbox is an active set strategy (also known as a projection method) similar to that of Gill et al., described in [20] and [19]. It has been modified for both Linear Programming (LP) and Quadratic Programming (QP) problems.
The solution procedure involves two phases. The first phase involves the calculation of a feasible point (if one exists). The second phase involves the generation of an iterative sequence of feasible points that converge to the solution. In this method an active set, 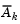 , is maintained that is an estimate of the active constraints (i.e., those that are on the constraint boundaries) at the solution point. Virtually all QP algorithms are active set methods. This point is emphasized because there exist many different methods that are very similar in structure but that are described in widely different terms.
, is maintained that is an estimate of the active constraints (i.e., those that are on the constraint boundaries) at the solution point. Virtually all QP algorithms are active set methods. This point is emphasized because there exist many different methods that are very similar in structure but that are described in widely different terms.
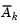 is updated at each iteration k, and this is used to form a basis for a search direction
is updated at each iteration k, and this is used to form a basis for a search direction 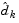 . Equality constraints always remain in the active set
. Equality constraints always remain in the active set 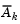 . The notation for the variable
. The notation for the variable 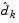 is used here to distinguish it from
is used here to distinguish it from 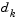 in the major iterations of the SQP method. The search direction
in the major iterations of the SQP method. The search direction 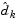 is calculated and minimizes the objective function while remaining on any active constraint boundaries. The feasible subspace for
is calculated and minimizes the objective function while remaining on any active constraint boundaries. The feasible subspace for 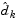 is formed from a basis
is formed from a basis 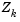 whose columns are orthogonal to the estimate of the active set
whose columns are orthogonal to the estimate of the active set 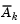 (i.e.,
(i.e., 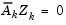 ). Thus a search direction, which is formed from a linear summation of any combination of the columns of
). Thus a search direction, which is formed from a linear summation of any combination of the columns of 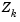 , is guaranteed to remain on the boundaries of the active constraints.
, is guaranteed to remain on the boundaries of the active constraints.
The matrix 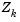 is formed from the last
is formed from the last 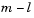 columns of the QR decomposition of the matrix
columns of the QR decomposition of the matrix 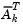 , where l is the number of active constraints and l < m. That is,
, where l is the number of active constraints and l < m. That is, 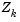 is given by
is given by
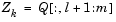
|
(3-33) |
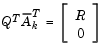
Once 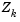 is found, a new search direction
is found, a new search direction 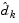 is sought that minimizes
is sought that minimizes 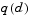 where
where 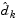 is in the null space of the active constraints. That is,
is in the null space of the active constraints. That is, 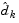 is a linear combination of the columns of
is a linear combination of the columns of 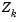 :
: 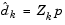 for some vector p.
for some vector p.
Then if you view the quadratic as a function of p, by substituting for 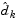 , you have
, you have
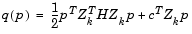
|
(3-34) |
Differentiating this with respect to p yields
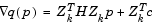
|
(3-35) |
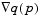 is referred to as the projected gradient of the quadratic function because it is the gradient projected in the subspace defined by
is referred to as the projected gradient of the quadratic function because it is the gradient projected in the subspace defined by 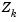 . The term
. The term 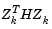 is called the projected Hessian. Assuming the Hessian matrix H is positive definite (which is the case in this implementation of SQP), then the minimum of the function q(p) in the subspace defined by
is called the projected Hessian. Assuming the Hessian matrix H is positive definite (which is the case in this implementation of SQP), then the minimum of the function q(p) in the subspace defined by 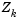 occurs when
occurs when 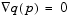 , which is the solution of the system of linear equations
, which is the solution of the system of linear equations
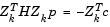
|
(3-36) |
A step is then taken of the form
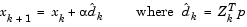
|
(3-37) |
At each iteration, because of the quadratic nature of the objective function, there are only two choices of step length 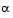 . A step of unity along
. A step of unity along 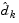 is the exact step to the minimum of the function restricted to the null space of
is the exact step to the minimum of the function restricted to the null space of 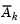 . If such a step can be taken, without violation of the constraints, then this is the solution to QP (Eq. 3-33). Otherwise, the step along
. If such a step can be taken, without violation of the constraints, then this is the solution to QP (Eq. 3-33). Otherwise, the step along 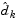 to the nearest constraint is less than unity and a new constraint is included in the active set at the next iteration. The distance to the constraint boundaries in any direction
to the nearest constraint is less than unity and a new constraint is included in the active set at the next iteration. The distance to the constraint boundaries in any direction 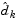 is given by
is given by
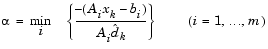
|
(3-38) |
which is defined for constraints not in the active set, and where the direction 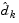 is towards the constraint boundary, i.e.,
is towards the constraint boundary, i.e., 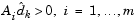 .
.
When n independent constraints are included in the active set, without location of the minimum, Lagrange multipliers, 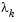 , are calculated that satisfy the nonsingular set of linear equations
, are calculated that satisfy the nonsingular set of linear equations
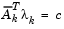
|
(3-39) |
If all elements of 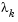 are positive,
are positive, 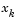 is the optimal solution of QP (Eq. 3-33). However, if any component of
is the optimal solution of QP (Eq. 3-33). However, if any component of 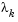 is negative, and the component does not correspond to an equality constraint, then the corresponding element is deleted from the active set and a new iterate is sought.
is negative, and the component does not correspond to an equality constraint, then the corresponding element is deleted from the active set and a new iterate is sought.
Initialization. The algorithm requires a feasible point to start. If the current point from the SQP method is not feasible, then you can find a point by solving the linear programming problem
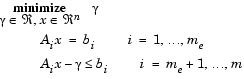
|
(3-40) |
The notation 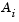 indicates the ith row of the matrix A. You can find a feasible point (if one exists) to Eq. 3-40 by setting x to a value that satisfies the equality constraints. You can determine this value by solving an under- or overdetermined set of linear equations formed from the set of equality constraints. If there is a solution to this problem, then the slack variable
indicates the ith row of the matrix A. You can find a feasible point (if one exists) to Eq. 3-40 by setting x to a value that satisfies the equality constraints. You can determine this value by solving an under- or overdetermined set of linear equations formed from the set of equality constraints. If there is a solution to this problem, then the slack variable 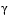 is set to the maximum inequality constraint at this point.
is set to the maximum inequality constraint at this point.
You can modify the preceding QP algorithm for LP problems by setting the search direction to the steepest descent direction at each iteration, where 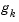 is the gradient of the objective function (equal to the coefficients of the linear objective function).
is the gradient of the objective function (equal to the coefficients of the linear objective function).
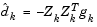
|
(3-41) |
If a feasible point is found using the preceding LP method, the main QP phase is entered. The search direction 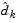 is initialized with a search direction
is initialized with a search direction 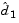 found from solving the set of linear equations
found from solving the set of linear equations
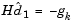
|
(3-42) |
where 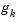 is the gradient of the objective function at the current iterate
is the gradient of the objective function at the current iterate 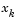 (i.e.,
(i.e., 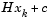 ).
).
If a feasible solution is not found for the QP problem, the direction of search for the main SQP routine 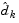 is taken as one that minimizes
is taken as one that minimizes 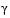 .
.
Line Search and Merit Function
The solution to the QP subproblem produces a vector 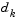 , which is used to form a new iterate
, which is used to form a new iterate
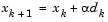
|
(3-43) |
The step length parameter 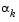 is determined in order to produce a sufficient decrease in a merit function. The merit function used by Han [24] and Powell [35] of the following form is used in this implementation.
is determined in order to produce a sufficient decrease in a merit function. The merit function used by Han [24] and Powell [35] of the following form is used in this implementation.
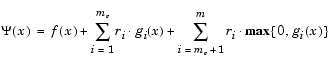
|
(3-44) |
Powell recommends setting the penalty parameter
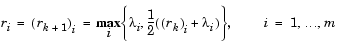
|
(3-45) |
This allows positive contribution from constraints that are inactive in the QP solution but were recently active. In this implementation, the penalty parameter 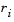 is initially set to
is initially set to
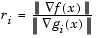
|
(3-46) |
where 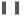 represents the Euclidean norm.
represents the Euclidean norm.
This ensures larger contributions to the penalty parameter from constraints with smaller gradients, which would be the case for active constraints at the solution point.
 | Quadratic Programming (QP) Subproblem | Multiobjective Optimization |  |