Optimization Toolbox

Quadratic Programming (QP) Subproblem

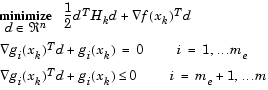
(3-28)

This subproblem can be solved using any QP algorithm (see, for instance, Quadratic Programming Solution). The solution is used to form a new iterate

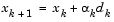
The step length parameter 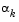is determined by an appropriate line search procedure so that a sufficient decrease in a merit function is obtained (see Updating the Hessian Matrix). The matrix 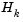is a positive definite approximation of the Hessian matrix of the Lagrangian function (Eq. 3-27). 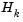can be updated by any of the quasi-Newton methods, although the BFGS method (see Updating the Hessian Matrix) appears to be the most popular.

A nonlinearly constrained problem can often be solved in fewer iterations than an unconstrained problem using SQP. One of the reasons for this is that, because of limits on the feasible area, the optimizer can make informed decisions regarding directions of search and step length.

Consider Rosenbrock's function (Eq. 3-2) with an additional nonlinear inequality constraint, g(x),

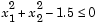
(3-29)

This was solved by an SQP implementation in 96 iterations compared to 140 for the unconstrained case. Figure 3-6 shows the path to the solution point 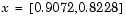starting at .

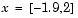Figure 3-6: SQP Method on Nonlinear Linearly Constrained Rosenbrock's Function (Eq.3-2)

Sequential Quadratic Programming (SQP)

SQP Implementation