Optimization Toolbox

Unconstrained Optimization

Although a wide spectrum of methods exists for unconstrained optimization, methods can be broadly categorized in terms of the derivative information that is, or is not, used. Search methods that use only function evaluations (e.g., the simplex search of Nelder and Mead [32]) are most suitable for problems that are very nonlinear or have a number of discontinuities. Gradient methods are generally more efficient when the function to be minimized is continuous in its first derivative. Higher order methods, such as Newton's method, are only really suitable when the second order information is readily and easily calculated, because calculation of second order information, using numerical differentiation, is computationally expensive.

Gradient methods use information about the slope of the function to dictate a direction of search where the minimum is thought to lie. The simplest of these is the method of steepest descent in which a search is performed in a direction,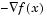, where 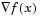is the gradient of the objective function. This method is very inefficient when the function to be minimized has long narrow valleys as, for example, is the case for Rosenbrock's function

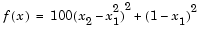
(3-2)

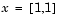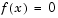The minimum of this function is at where . A contour map of this function is shown in Figure 3-1, along with the solution path to the minimum for a steepest descent implementation starting at the point [-1.9,2]. The optimization was terminated after 1000 iterations, still a considerable distance from the minimum. The black areas are where the method is continually zigzagging from one side of the valley to another. Note that toward the center of the plot, a number of larger steps are taken when a point lands exactly at the center of the valley.

Figure 3-1: Steepest Descent Method on Rosenbrock's Function (Eq. 2-2)

This type of function (Eq. 3-2), also known as the banana function, is notorious in unconstrained examples because of the way the curvature bends around the origin. Eq. 3-2 is used throughout this section to illustrate the use of a variety of optimization techniques. The contours have been plotted in exponential increments because of the steepness of the slope surrounding the U-shaped valley.

This section continues with discussions of the following:

• Quasi-Newton Methods
• Line Search
• Quasi-Newton Implementation

Optimization Overview

Quasi-Newton Methods