

| Optimization Toolbox |   |
Line Search
Most unconstrained and constrained methods use the solution of a subproblem to yield a search direction in which the solution is estimated to lie. The minimum along the line formed from this search direction is generally approximated using a search procedure (e.g., Fibonacci, Golden Section) or by a polynomial method involving interpolation or extrapolation (e.g., quadratic, cubic). Polynomial methods approximate a number of points with a univariate polynomial whose minimum can be calculated easily. Interpolation refers to the condition that the minimum is bracketed (i.e., the minimum lies in the area spanned by the available points), whereas extrapolation refers to a minimum located outside the range spanned by the available points. Extrapolation methods are generally considered unreliable for estimating minima for nonlinear functions. However, they are useful for estimating step length when you are trying to bracket the minimum as shown in Line Search Procedures. Polynomial interpolation methods are generally the most effective in terms of efficiency when the function to be minimized is continuous. The problem is to find a new iterate 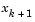 of the form
of the form
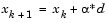
|
(3-8) |
where 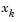 denotes the current iterate, d is the search direction obtained by an appropriate method, and
denotes the current iterate, d is the search direction obtained by an appropriate method, and 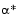 is a scalar step length parameter that is the distance to the minimum.
is a scalar step length parameter that is the distance to the minimum.
Quadratic Interpolation
Quadratic interpolation involves a data fit to a univariate function of the form
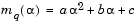
|
(3-9) |
where an extremum occurs at a step length of
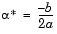
|
(3-10) |
This point can be a minimum or a maximum. It is a minimum when interpolation is performed (i.e., using a bracketed minimum) or when a is positive. Determination of coefficients a and b can be found using any combination of three gradient or function evaluations. It can also be carried out with just two gradient evaluations. The coefficients are determined through the formulation and solution of a linear set of simultaneous equations. Various simplifications in the solution of these equations can be achieved when particular characteristics of the points are used. For example, the first point can generally be taken as 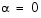 . Other simplifications can be achieved when the points are evenly spaced. A general problem formula is as follows.
. Other simplifications can be achieved when the points are evenly spaced. A general problem formula is as follows.
Given three unevenly spaced points 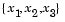 and their associated function values
and their associated function values 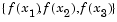 the minimum resulting from a second-order fit is given by
the minimum resulting from a second-order fit is given by
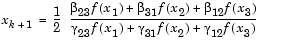
|
(3-11) |
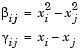
For interpolation to be performed, as opposed to extrapolation, the minimum must be bracketed so that the points can be arranged to give
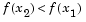 and
and 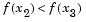
Cubic Interpolation
Cubic interpolation is useful when gradient information is readily available or when more than three function evaluations have been calculated. It involves a data fit to the univariate function
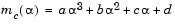
|
(3-12) |
where the local extrema are roots of the quadratic equation
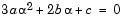
To find the minimum extremum, take the root that gives 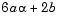 as positive. You can determine coefficients a and b using any combination of four gradient or function evaluations or, alternatively, with just three gradient evaluations.
as positive. You can determine coefficients a and b using any combination of four gradient or function evaluations or, alternatively, with just three gradient evaluations.
The coefficients are calculated by the formulation and solution of a linear set of simultaneous equations. A general formula, given two points, 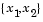 , their corresponding gradients with respect to x,
, their corresponding gradients with respect to x, 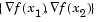 , and associated function values,
, and associated function values, 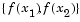 , is
, is
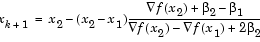
|
(3-13) |
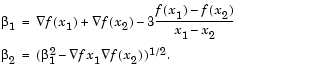
 | Quasi-Newton Methods | Quasi-Newton Implementation |  |