| Optimization Toolbox | |
Quasi-Newton Implementation
A quasi-Newton algorithm is used in fminunc. The algorithm consists of two phases:
Implementation details of the two phases are discussed below.
Hessian Update
The direction of search is determined by a choice of either the BFGS (Eq. 3-6) or the DFP method given in Quasi-Newton Methods (set the options parameter HessUpdate to 'dfp' to select the DFP method). The Hessian, H, is always maintained to be positive definite so that the direction of search, d, is always in a descent direction. This means that for some arbitrarily small step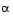 
in the direction d, the objective function decreases in magnitude. You achieve positive definiteness of H by ensuring that H is initialized to be positive definite and thereafter 
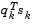(from Eq. 3-14) is always positive. The term 
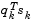is a product of the line search step length parameter 
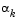and a combination of the search direction d with past and present gradient evaluations,
|
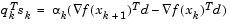
(3-14) |
You always achieve the condition that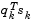 
is positive by performing a sufficiently accurate line search. This is because the search direction, d, is a descent direction, so that 
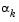and 
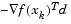are always positive. Thus, the possible negative term 
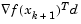can be made as small in magnitude as required by increasing the accuracy of the line search.
Line Search Procedures
Two line search strategies are used, depending on whether gradient information is readily available or whether it must be calculated using a finite difference method. When gradient information is available, the default is to use a cubic polynomial method. When gradient information is not available, the default is to use a mixed quadratic and cubic polynomial method.
Cubic Polynomial Method . In the proposed cubic polynomial method, a gradient and a function evaluation are made at every iteration k. At each iteration an update is performed when a new point is found,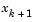 
, that satisfies the condition
|
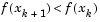
(3-15) |
At each iteration a step,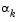 
, is attempted to form a new iterate of the form
|
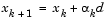
(3-16) |
If this step does not satisfy the condition (Eq. 3-15), then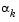 
is reduced to form a new step, 
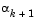. The usual method for this reduction is to use bisection, i.e., to continually halve the step length until a reduction is achieved in f(x). However, this procedure is slow when compared to an approach that involves using gradient and function evaluations together with cubic interpolation/extrapolation methods to identify estimates of step length.
When a point is found that satisfies the condition (Eq. 3-15), an update is performed if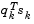 
is positive. If it is not, then further cubic interpolations are performed until the univariate gradient term 
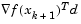is sufficiently small so that 
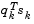is positive.
It is usual practice to reset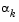 
to unity after every iteration. However, note that the quadratic model (Eq. 3-3) is generally only a good one near to the solution point. Therefore, 
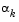is modified at each major iteration to compensate for the case when the approximation to the Hessian is monotonically increasing or decreasing. To ensure that, as 
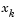approaches the solution point, the procedure reverts to a value of 
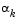close to unity, the values of 
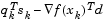and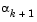 
are used to estimate the closeness to the solution point and thus to control the variation in 
.
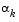Cubic Polynomial Line Search Procedures. After each update procedure, a step length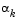 
is attempted, following which a number of scenarios are possible. Consideration of all the possible cases is quite complicated and so they are represented pictorially below.
.
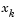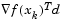, which is always negative for the left point.
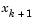after a step of 
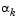is taken in the direction d.
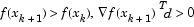
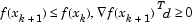
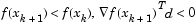
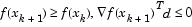where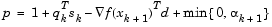 
Cases 1 and 2 show the procedures performed when the value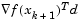 
is positive. Cases 3 and 4 show the procedures performed when the value 
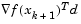is negative. The notation 
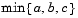refers to the smallest value of the set 
.
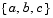At each iteration a cubicly interpolated step length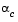 
is calculated and then used to adjust the step length parameter 
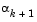. Occasionally, for very nonlinear functions 
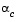can be negative, in which case 
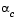is given a value of 
.
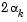Certain robustness measures have also been included so that, even in the case when false gradient information is supplied, you can achieve a reduction in f(x) by taking a negative step. You do this by setting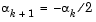 
when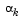 
falls below a certain threshold value (e.g., 1e-8). This is important when extremely high precision is required, if only finite difference gradients are available.
Mixed Cubic/Quadratic Polynomial Method. The cubic interpolation/extrapolation method has proved successful for a large number of optimization problems. However, when analytic derivatives are not available, evaluating finite difference gradients is computationally expensive. Therefore, another interpolation/extrapolation method is implemented so that gradients are not needed at every iteration. The approach in these circumstances, when gradients are not readily available, is to use a quadratic interpolation method. The minimum is generally bracketed using some form of bisection method. This method, however, has the disadvantage that all the available information about the function is not used. For instance, a gradient calculation is always performed at each major iteration for the Hessian update. Therefore, given three points that bracket the minimum, it is possible to use cubic interpolation, which is likely to be more accurate than using quadratic interpolation. Further efficiencies are possible if, instead of using bisection to bracket the minimum, extrapolation methods similar to those used in the cubic polynomial method are used.
Hence, the method that is used in fminunc, lsqnonlin, lsqcurvefit, and fsolve is to find three points that bracket the minimum and to use cubic interpolation to estimate the minimum at each line search. The estimation of step length at each minor iteration, j, is shown in the following graphs for a number of point combinations. The left-most point in each graph represents the function value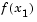 
and univariate gradient 
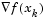obtained at the last update. The remaining points represent the points accumulated in the minor iterations of the line search procedure.
The terms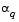 
and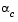 
refer to the minimum obtained from a respective quadratic and cubic interpolation or extrapolation. For highly nonlinear functions, 
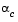and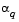 
can be negative, in which case they are set to a value of 
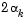so that they are always maintained to be positive. Cases 1 and 2 use quadratic interpolation with two points and one gradient to estimate a third point that brackets the minimum. If this fails, cases 3 and 4 represent the possibilities for changing the step length when at least three points are available.
When the minimum is finally bracketed, cubic interpolation is achieved using one gradient and three function evaluations. If the interpolated point is greater than any of the three used for the interpolation, then it is replaced with the point with the smallest function value. Following the line search procedure, the Hessian update procedure is performed as for the cubic polynomial line search method.
The following graphs illustrate the line search procedures for cases 1 through 4, with a gradient only for the first point.
| | Line Search | Least-Squares Optimization | |
