| Optimization Toolbox | |
Least-Squares Optimization
The line search procedures used in conjunction with a quasi-Newton method are used in the function fminunc. They are also used as part of the nonlinear least-squares (LS) optimization routines, lsqnonlin and lsqcurvefit. In the least-squares problem a function f(x) is minimized that is a sum of squares.
|
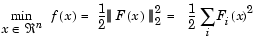
(3-17) |
Problems of this type occur in a large number of practical applications, especially when fitting model functions to data, i.e., nonlinear parameter estimation. They are also prevalent in control where you want the output,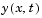 
, to follow some continuous model trajectory, 
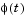, for vector x and scalar t. This problem can be expressed as
|
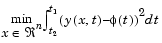
(3-18) |
where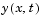 
and 
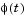are scalar functions.
When the integral is discretized using a suitable quadrature formula, Eq. 3-18 can be formulated as a least-squares problem
|
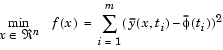
(3-19) |
where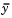 
and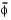 
include the weights of the quadrature scheme. Note that in this problem the vector F(x) is
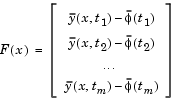
In problems of this kind, the residual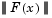 
is likely to be small at the optimum since it is general practice to set realistically achievable target trajectories. Although the function in LS (Eq. 3-18) can be minimized using a general unconstrained minimization technique, as described in Unconstrained Optimization, certain characteristics of the problem can often be exploited to improve the iterative efficiency of the solution procedure. The gradient and Hessian matrix of LS (Eq. 3-18) have a special structure.
Denoting the m-by-n Jacobian matrix of F(x) as J(x), the gradient vector of f(x) as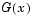 
, the Hessian matrix of f(x) as 
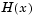, and the Hessian matrix of each 
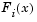as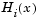 
, you have
|
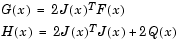
(3-20) |
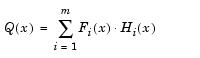
The matrix Q(x) has the property that when the residual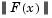 
tends to zero as 
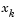approaches the solution, then Q(x) also tends to zero. Thus when 
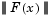is small at the solution, a very effective method is to use the Gauss-Newton direction as a basis for an optimization procedure.
This section continues with discussions of the following:
| | Quasi-Newton Implementation | Gauss-Newton Method | |