| Optimization Toolbox | |
Nonlinear Least-Squares Implementation
For a general survey of nonlinear least-squares methods, see Dennis [10]. Specific details on the Levenberg-Marquardt method can be found in Moré [30]. Both the Gauss-Newton method and the Levenberg-Marquardt method are implemented in the Optimization Toolbox. Details of the implementations are discussed below:
Gauss-Newton Implementation
The Gauss-Newton method is implemented using polynomial line search strategies similar to those discussed for unconstrained optimization. In solving the linear least-squares problem (Eq. 3-18), you can avoid exacerbation of the conditioning of the equations by using the QR decomposition of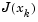 
and applying the decomposition to 
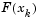(using the MATLAB \ operator). This is in contrast to inverting the explicit matrix, 
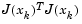, which can cause unnecessary errors to occur.
Robustness measures are included in the method. These measures consist of changing the algorithm to the Levenberg-Marquardt method when either the step length goes below a threshold value (1e-15 in this implementation) or when the condition number of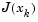 
is below 1e-10. The condition number is a ratio of the largest singular value to the smallest.
Levenberg-Marquardt Implementation
The main difficulty in the implementation of the Levenberg-Marquardt method is an effective strategy for controlling the size of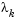 
at each iteration so that it is efficient for a broad spectrum of problems. The method used in this implementation is to estimate the relative nonlinearity of 
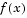using a linear predicted sum of squares 
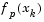and a cubicly interpolated estimate of the minimum 
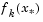. In this way the size of 
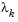is determined at each iteration.
The linear predicted sum of squares is calculated as
|
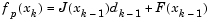
(3-23) |
and the term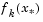 
is obtained by cubicly interpolating the points 
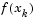and 
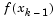. A step length parameter 
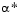is also obtained from this interpolation, which is the estimated step to the minimum. If 
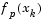is greater than 
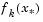, then 
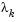is reduced, otherwise it is increased. The justification for this is that the difference between 
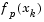and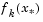 
is a measure of the effectiveness of the Gauss-Newton method and the linearity of the problem. This determines whether to use a direction approaching the steepest descent direction or the Gauss-Newton direction. The formulas for the reduction and increase in 
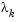, which have been developed through consideration of a large number of test problems, are shown in the following figure.
Following the update of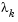 
, a solution of Eq. 3-22 is used to obtain a search direction, 
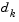. A step length of unity is then taken in the direction 
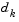, which is followed by a line search procedure similar to that discussed for the unconstrained implementation. The line search procedure ensures that 
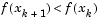at each major iteration and the method is therefore a descent method.
The implementation has been successfully tested on a large number of nonlinear problems. It has proved to be more robust than the Gauss-Newton method and iteratively more efficient than an unconstrained method. The Levenberg-Marquardt algorithm is the default method used by lsqnonlin. You can select the Gauss-Newton method by setting the options parameter LevenbergMarquardt to 'off'.
| | Levenberg-Marquardt Method | Nonlinear Systems of Equations | |
k