Optimization Toolbox

Nonlinear Systems of Equations

Solving a nonlinear system of equations 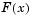involves finding a solution such that every equation in the nonlinear system is 0. That is, we have 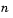equations and 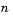unknowns and we want to find 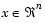such that 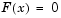where

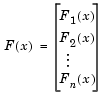
The assumption is that a zero, or root, of the system exists. These equations may represent economic constraints, for example, that must all be satisfied.

Gauss-Newton Method

One approach to solving this problem is to use a Nonlinear Least-Squares solver, such those described in Least-Squares Optimization. Since we assume the system has a root, it would have a small residual, and so using the Gauss-Newton Method is effective. In this case, at each iteration we solve a linear least-squares problem, as described in Eq. 3-21, to find the search direction. (See Gauss-Newton Method for more information.)

Trust-Region Dogleg Method

Another approach is to solve a linear system of equations to find the search direction, namely, Newton's method says to solve for the search direction 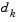such that

where is the n-by-n Jacobian

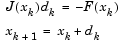
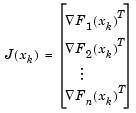
Newton's method can run into difficulties. 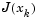may be singular, and so the Newton step 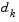is not even defined. Also, the exact Newton step 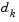may be expensive to compute. In addition, Newton's method may not converge if the starting point is far from the solution.

Using trust-region techniques (introduced in Trust-Region Methods for Nonlinear Minimization) improves robustness when starting far from the solution and handles the case when 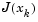is singular. To use a trust-region strategy, a merit function is needed to decide if 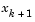is better or worse than 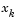. A possible choice is

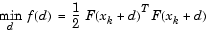
But a minimum of 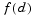is not necessarily a root of .

The Newton step is a root of

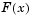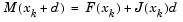
and so it is also a minimum of 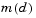where

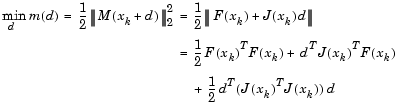
(3-24)

Then 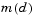is a better choice of merit function than 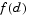, and so the trust region subproblem is

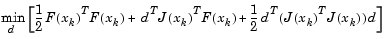
(3-25)

such that 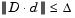. This subproblem can be efficiently solved using a dogleg strategy.

For an overview of trust-region methods, see Conn [5], and Nocedal [33].

Nonlinear Least-Squares Implementation

Nonlinear Equations Implementation