

| Optimization Toolbox |   |
Nonlinear Equations Implementation
Both the Gauss-Newton and trust-region dogleg methods are implemented in the Optimization Toolbox. Details of their implementations are discussed below.
Gauss-Newton Implementation
The Gauss-Newton implementation is the same as that for least-squares optimization. It is described in Gauss-Newton Implementation.
Trust-Region Dogleg Implementation
The key feature of this algorithm is the use of the Powell dogleg procedure for computing the step 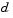 , which minimizes Eq. 3-25. For a detailed description, see Powell [36].
, which minimizes Eq. 3-25. For a detailed description, see Powell [36].
The step 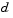 is constructed from a convex combination of a Cauchy step (a step along the steepest descent direction) and a Gauss-Newton step for
is constructed from a convex combination of a Cauchy step (a step along the steepest descent direction) and a Gauss-Newton step for 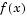 . The Cauchy step is calculated as
. The Cauchy step is calculated as
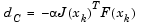
where 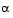 is chosen to minimize Eq. 3-24.
is chosen to minimize Eq. 3-24.
The Gauss-Newton step is calculated by solving
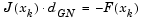
using the MATLAB \ (matrix left division) operator.
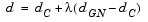
where  is the largest value in the interval [0,1] such that
is the largest value in the interval [0,1] such that 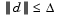 . If
. If 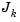 is (nearly) singular,
is (nearly) singular, 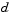 is just the Cauchy direction.
is just the Cauchy direction.
The dogleg algorithm is efficient since it requires only one linear solve per iteration (for the computation of the Gauss-Newton step). Additionally, it can be more robust than using the Gauss-Newton method with a line search.
 | Nonlinear Systems of Equations | Constrained Optimization |  |