

| Optimization Toolbox |   |
Goal Attainment Method
The method described here is the Goal Attainment method of Gembicki [18]. This involves expressing a set of design goals, 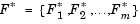 , which is associated with a set of objectives,
, which is associated with a set of objectives,
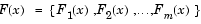 . The problem formulation allows the objectives to be under- or overachieved, enabling the designer to be relatively imprecise about initial design goals. The relative degree of under- or overachievement of the goals is controlled by a vector of weighting coefficients,
. The problem formulation allows the objectives to be under- or overachieved, enabling the designer to be relatively imprecise about initial design goals. The relative degree of under- or overachievement of the goals is controlled by a vector of weighting coefficients,  , and is expressed as a standard optimization problem using the following formulation.
, and is expressed as a standard optimization problem using the following formulation.
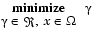
|
(3-53) |
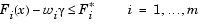
The term 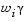 introduces an element of slackness into the problem, which otherwise imposes that the goals be rigidly met. The weighting vector, w, enables the designer to express a measure of the relative tradeoffs between the objectives. For instance, setting the weighting vector w equal to the initial goals indicates that the same percentage under- or overattainment of the goals,
introduces an element of slackness into the problem, which otherwise imposes that the goals be rigidly met. The weighting vector, w, enables the designer to express a measure of the relative tradeoffs between the objectives. For instance, setting the weighting vector w equal to the initial goals indicates that the same percentage under- or overattainment of the goals, 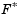 , is achieved. You can incorporate hard constraints into the design by setting a particular weighting factor to zero (i.e.,
, is achieved. You can incorporate hard constraints into the design by setting a particular weighting factor to zero (i.e., 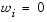 ). The Goal Attainment method provides a convenient intuitive interpretation of the design problem, which is solvable using standard optimization procedures. Illustrative examples of the use of the Goal Attainment method in control system design can be found in Fleming ([12],[13]).
). The Goal Attainment method provides a convenient intuitive interpretation of the design problem, which is solvable using standard optimization procedures. Illustrative examples of the use of the Goal Attainment method in control system design can be found in Fleming ([12],[13]).
The Goal Attainment method is represented geometrically in Figure 3-12, Geometrical Representation of Goal Attainment Method, for the two-dimensional problem.
Figure 3-12: Geometrical Representation of Goal Attainment Method
Specification of the goals, 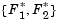 , defines the goal point, P. The weighting vector defines the direction of search from P to the feasible function space,
, defines the goal point, P. The weighting vector defines the direction of search from P to the feasible function space, 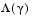 . During the optimization
. During the optimization 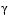 is varied, which changes the size of the feasible region. The constraint boundaries converge to the unique solution point
is varied, which changes the size of the feasible region. The constraint boundaries converge to the unique solution point 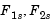 .
.
 | Introduction | Algorithm Improvements for Goal Attainment Method |  |