Optimization Toolbox

Algorithm Improvements for Goal Attainment Method

The Goal Attainment method has the advantage that it can be posed as a nonlinear programming problem. Characteristics of the problem can also be exploited in a nonlinear programming algorithm. In Sequential Quadratic Programming (SQP), the choice of merit function for the line search is not easy because, in many cases, it is difficult to "define" the relative importance between improving the objective function and reducing constraint violations. This has resulted in a number of different schemes for constructing the merit function (see, for example, Schittkowski [38]). In Goal Attainment programming there might be a more appropriate merit function, which you can achieve by posing Eq. 3-53 as the minimax problem

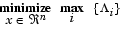
(3-54)

where

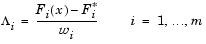
Following the argument of Brayton et al. [2] for minimax optimization using SQP, using the merit function of Eq. 3-44 for the Goal Attainment problem of Eq. 3-54 gives

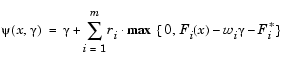
(3-55)

When the merit function of Eq. 3-55 is used as the basis of a line search procedure, then, although 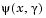might decrease for a step in a given search direction, the function max 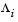might paradoxically increase. This is accepting a degradation in the worst case objective. Since the worst case objective is responsible for the value of the objective function 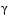, this is accepting a step that ultimately increases the objective function to be minimized. Conversely, 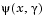might increase when max 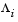decreases, implying a rejection of a step that improves the worst case objective.

Following the lines of Brayton et al. [2], a solution is therefore to set 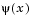equal to the worst case objective, i.e.,

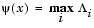
(3-56)

A problem in the Goal Attainment method is that it is common to use a weighting coefficient equal to zero to incorporate hard constraints. The merit function of Eq. 3-56 then becomes infinite for arbitrary violations of the constraints. To overcome this problem while still retaining the features of Eq. 3-56, the merit function is combined with that of Eq. 3-45, giving the following

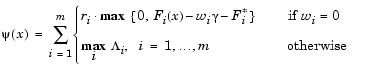
(3-57)

Another feature that can be exploited in SQP is the objective function 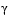. From the KT equations (Eq. 3-26) it can be shown that the approximation to the Hessian of the Lagrangian, H, should have zeros in the rows and columns associated with the variable 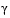. Hoever, this property doe snot appear if H is initialized as the identity matrix. H is therefore initialized and maintained to have zeros in the rows and columns associated with .

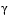These changes make the Hessian, H, indefinite, therefore H is set to have zeros in the rows and columns associated with 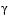, except for the diagonal element, which is set to a small positive number (e.g., 1e-10). This allows use of the fast converging positive definite QP method described in Quadratic Programming Solution.

The preceding modifications have been implemented in fgoalattain and have been found to make the method more robust. However, because of the rapid convergence of the SQP method, the requirement that the merit function strictly decrease sometimes requires more function evaluations than an implementation of SQP using the merit function of Eq. 3-44.

Goal Attainment Method

Selected Bibliography