idfrd (System Identification Toolbox)

Create the idfrd (Identified Frequency Response Data) object that stores frequency function and spectrum data along with covariance information.

Syntax

h = idfrd(Response,Freqs,Ts)
h = idfrd(Response,Freqs,Ts,'CovarianceData',Covariance, ... 
'SpectrumData',Spec,'NoiseCovariance',Speccov,'property1', ... 
 Value1,'PropertyN',ValueN)
h = idfrd(mod)
h = idfrd(mod,Freqs)

Description

idfrd creates the idfrd model object.

For a model

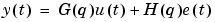
stores the transfer function estimate G (see equation (Equation 3-4) in the "Tutorial" chapter)

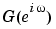
as well as the spectrum of the additive noise (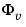) at the outputs

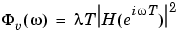
where 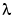is the estimated variance of e(t), and T is the sampling interval.

Creating idfrd from Given Responses

Response is a 3-D array of dimension ny-by-nu-by-Nf with ny being the number of outputs, nu the number of inputs, and Nf the number of frequencies (i.e., the length of Freqs). Response(ky,ku,kf) is thus the complex-valued frequency response from input ku to output ky at frequency 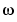=Freqs(kf). When defining the response of a SISO system, Response can be given as a vector.

Freqs is a column vector of length Nf containing the frequencies of the response.

Ts is the sampling interval. T = 0 means a continuous time model.

Covariance is a 5-D array containing the covariance of the frequency response. It has dimension ny-by-nu-by-Nf-by-2-by-2. The structure is such that Covariance(ky,ku,kf,:,:) is the 2-by-2 covariance matrix of the response Response(ky,ku,kf). The 1-1 element is the variance of the real part, the 2-2 element is the variance of the imaginary part and the 1-2 and 2-1 elements is the covariance between the real and imaginary parts. squeeze(Covariance(ky,ku,kf,:,:)) thus gives the covariance matrix of the corresponding response.

The information about spectrum is optional. The format is as follows:

spec is a 3-D array of dimension ny-by-ny-by-Nf, such that spec(ky1,ky2,kf) is the cross spectrum between the noise at output ky1 and the noise at output ky2, at frequency Freqs(kf). When ky1=ky2 the (power) spectrum of the noise at output ky1 is thus obtained. For a single output model, spec can be given as a vector.

speccov is a 3-D array of dimension ny-by-ny-by-Nf, such that speccov(ky1,ky1,kf) is the variance of the corresponding power spectrum. Normally, no information is included about the covariance of the non-diagonal spectrum elements.

If only SpectrumData is to be packaged in the idfrd object, set Response = [].

Creating idfrd from a Given Model

idfrd can also be computed from a given model mod (defined as any idmodel object).

The default values of the frequencies in the discrete-time case are

```
Freqs = [1:128]'/128*pi/Ts
```

where Ts is the sampling interval specified by mod and for the continuous-time case

Freqs = logspace(log10(pi/Ts/100),log10(10*pi/ Ts),128)

where Ts is the sampling interval of the data from which the model was estimated. If the model is not estimated, a simple default choice of Freqs is made. In this case it may be necessary to supply the argument Freqs explicitly.

If mod has InputDelay different from zero, these are appended as phase lags, and h will then have an InputDelay 0.

The estimated covariances are computed using the Gauss approximation formula from the uncertainty information in mod. For models with complicated parameter dependencies, numerical differentiation is applied. The step-sizes for the numerical derivatives are determined by nuderst.

Frequency responses for submodels can be obtained by the standard subreferencing: h = idfrd(m(2,3)). See idmodel. In particular, h= idfrf(m('measured')) gives h that just contains the ResponseData (G) and no spectra. Also h = idfrd(m('noise')) gives a h that just contains SpectrumData.

The idfrd models can be graphed with bode, ffplot, and nyquist, which all accept mixtures of idmodel and idfrd models as arguments. Note that spa and etfe return their estimation results as idfrd objects.

idfrd Properties

To summarize the properties of idfrd:

ResponseData: A 3-D array of the complex-valued frequency response as described above. For SISO system use Response(1,1,:) to obtain a vector of the response data.
Frequency: A column vector containing the frequencies as which the responses are defined.
CovarianceData: A 5-D array of the covariance matrices of the response data as described above.
SpectrumData: A 3-D array containing power spectra and cross spectra of the output disturbances (noise) of the system.
NoiseCovariance: A 3-D array containing the variances of the power spectra, as explained above.
Units: the unit of the frequency vector. Can assume the values `rad/s' and 'Hz'.
Ts: A scalar denoting the sampling interval of the model whose frequency response is stored. 'Ts' = 0 means a continuous-time model.
Name: An optional name for the object
InputName: A string or a cell array containing the names of the input channels. It has as many entries as there are input channels.
OutputName: Correspondingly for the output channels.
InputUnit: The units in which the input channels are measured. It has the same format as 'InputName'.
OutputUnit: Correspondingly for the output channels.
InputDelay: A row vector of length equal to the number of input channels. Contains the delays from the input channels. These should thus be appended as phase lags when the response is calculated. This is done automatically by freqresp, bode, ffplot, and nyquist. Note that if the idfrd is calculated form an idmodel, possible input delays in that model are converted to phase lags, and InputDelay of the idfrd model is set to zero.
Notes: An arbitrary field to store extra information and notes about the object.
UserData: An arbitrary field for any possible use.
EstimationInfo: A structure that contains information about the estimation process that is behind the frequency data. It contains the following fields:

Status: Gives the status of the model, e.g., 'Not estimated'.
Method: The identification routine that created the model.
WindowSize: If the model was estimated by spa or etfe, the size of window (input argument M) that was used.
DataName: The name of the data set from which the model was estimated.
DataLength: The length of this data set.

Note that all properties can be set or retrieved either by set/get or by subscripts. Autofill applies to all properties and values, and these are case insensitive:

h.ts = 0
loglog(h.fre,squeeze(h.spe(2,2,:)))

For a complete list of property values, use get(m). To see possible value assignments, use set(m). See also idprops idfrd.

Subreferencing

The different channels of the idfrd are retrieved by subreferencing.

```
h(outputs,inputs)
```

h(2,3) thus contains the response data from input channel 3 to output channel 2, and, if applicable, the output spectrum data for output channel 2. The channels can also be referred to by their names h('power',{'voltage',''speed'}).

```
h('m') 
```

contains the information for measured inputs only, that is, just ResponseData, while

```
h('n')
```

('n' for 'noise') just contains SpectrumData.

Horizontal Concatenation

Adding input channels

```
h = [h1,h2,...,hN]
```

creates an idfrd model h, with ResponseData containing of all the input channels in h1,... hN. The output channels of hk must be the same as well as the frequency vectors. SpectrumData will be ignored.

Vertical Concatenation

Adding output channels

```
h = [h1;h2;... ;hN]
```

creates an idfrd model h with ResponseData containing all the output channels in h1, h2,...,hN. The input channels of hk must all be the same, as well as the frequency vectors. SpectrumData will also be appended for the new outputs. The cross spectrum between output channels will then be set to zero.

Examples

Compare the results from spectral analysis and an ARMAX model.

m = armax(z,[2 2 2 1]);
g = spa(z)
bode(g,m)

Compute separate idfrd models, one containing g and the other the noise spectrum.

```
g = idfrd(m('m'))
phi = idfrd(m('n'))
```

idfilt idgrey