etfe (System Identification Toolbox)

System Identification Toolbox

etfe

Estimate empirical transfer functions and periodograms.

Syntax

```
g = etfe(data)
g = etfe(data,M,N)
```

Description

etfe estimates the transfer function g of the general linear model

data contains the output-input data and is an iddata object.

g is given as an idfrd object with the estimate of 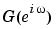at the frequencies

```
w = [1:N]/N*pi/T
```

The default value of N is 128.

In case data contains a time series (no input channels), g is returned as the periodogram of y.

When M is specified other than the default value M = [], a smoothing operation is performed on the raw spectral estimates. The effect of M is then similar to the effect of M in spa. This can be a useful alternative to spa for narrowband spectra and systems, which require large values of M.

When etfe is applied to time series, the corresponding spectral estimate is normalized in the way that is defined in the section Spectrum Normalization and the Sampling Interval in the Tutorial. Note that this normalization may differ from the one used by spectrum in the Signal Processing Toolbox.

If the (input) data is marked as periodic (data.Period = integer) and contains an even number of periods, the response is computed at the frequencies k*2*pi/period for k=0 up to the Nyquist frequency.

Examples

Compare an empirical transfer function estimate to a smoothed spectral estimate.

```
ge = etfe(z);
gs = spa(z);
bode(ge,gs)
```

Generate a periodic input, simulate a system with it, and compare the frequency response of the estimated model with the true system at the excited frequency points.

m = idpoly([1 -1.5 0.7],[0 1 0.5]);
u = iddata([],idinput([50,1,10],'sine'));
u.Period = 50;
y = sim(m,u);
me = etfe([y u])
bode(me,'b*',m)

Algorithm

The empirical transfer function estimate is computed as the ratio of the output Fourier transform to the input Fourier transform, using fft. The periodogram is computed as the normalized absolute square of the Fourier transform of the time series.

The smoothed versions (M less than the length of z) are obtained by applying a Hamming window to the output fast Fourier transform (FFT) times the conjugate of the input FFT, and to the absolute square of the input FFT, respectively, and subsequently forming the ratio of the results. The length of this Hamming window is equal to the number of data points in z divided by M, plus one.

See Also

spa

EstimationInfo ffplot