System Identification Toolbox

ARMAX, Output-Error and Box-Jenkins Models

There are several elaborations of the basic ARX model, where different disturbance models are introduced. These include well known model types, such as ARMAX, Output-Error, and Box-Jenkins.

The General Structure

A general input-output linear model for a single-output system with input u and output y can be written

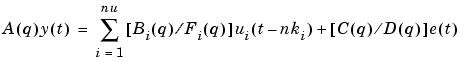
Here u_i denotes input #i, and A, B_i, C, D, and F_i, are polynomials in the shift operator (z or q). (Don't get intimidated by this: It is just a compact way of writing difference equations; see below.)

The general structure is defined by giving the time-delays nk and the orders of these polynomials (i.e., the number of poles and zeros of the dynamic model from u to y, as well as of the disturbance model from e to y).

The Special Cases

Most often the choices are confined to one of the following special cases.

ARX:

ARMAX:

OE:

(Output-Error)

BJ:

(Box-Jenkins)

The "shift operator polynomials" are just compact ways of writing difference equations. For example the ARMAX model in longhand would be

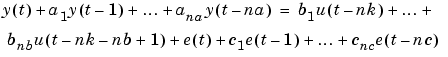
Note that A(q) corresponds to poles that are common between the dynamic model and the disturbance model (useful if disturbances enter the system "close to" the input). Likewise 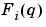determines the poles that are unique for the dynamics from input # i, and D(q) the poles that are unique for the disturbances.

The reason for introducing all these model variants is to provide for flexibility in the disturbance description and to allow for common or different poles (dynamics) for the different inputs.

Entering the Model Structure

Use the Structure pop-up menu in the Parametric Models dialog to choose between the ARX, ARMAX, Output-Error, and Box-Jenkins structures. Note that if the Working Data set has several outputs, only the first choice is available. For time series (data with no input signal) only AR and ARMA are available among these choices. These are the time series counterparts of ARX and ARMAX.

The orders of the polynomials are selected by the pop-up menus in the Order Editor dialog window, or by directly entering them in the edit box Orders in the Parametric Models window. When the order editor is open, the default orders, entered as you change the model structure, are based on previously used orders.

Estimation Method

The coefficients of the polynomials are estimated using a prediction error/Maximum Likelihood method, by minimizing the size of the error term "e" in the expression above. Several options govern the minimization procedure. These are accessed by activating Iteration Control in the Parametric Models window, and selecting Options.

The algorithms are further described in Function Reference under armax, Algorithm Properties, bj, oe, and pem. See also Parametric Model Estimation and Defining Model Structures.

Note    These model structures are available only for the scalar output case. For multi-output models, the state-space structures offer the same flexibility. Also note that it is not possible to estimate many different structures simultaneously for the input-output models.

ARX Models

State-Space Models