System Identification Toolbox

ARX Models

The Structure

The most used model structure is the simple linear difference equation

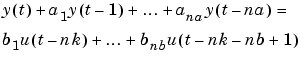
which relates the current output y(t) to a finite number of past outputs y(t-k) and inputs u(t-k).

The structure is thus entirely defined by the three integers na, nb, and nk. na is equal to the number of poles and nb-1 is the number of zeros, while nk is the pure time-delay (the dead-time) in the system. For a system under sampled-data control, typically nk is equal to 1 if there is no dead-time.

For multi-input systems nb and nk are row vectors, where the i-th element gives the order/delay associated with the i-th input.

Entering the Order Parameters

The orders na, nb, and nk can either be directly entered into the edit box Orders in the Parametric Models window, or selected using the pop-up menus in the Order Editor.

Estimating Many Models Simultaneously

By entering any or all of the structure parameters as vectors, using MATLAB's colon notation, like na=1:10, etc., you define many different structures that correspond to all combinations of orders. When selecting Estimate, models corresponding to all of these structures are computed. A special plot window will then open that shows the fit of these models to Validation Data. By clicking in this plot, you can then enter any models of your choice into the Model Board.

Multi-input models: For multi-input models you can of course enter each of the input orders and delays as a vector. The number of models resulting from all combinations of orders and delays can however be very large. As an alternative, you may enter one vector (like nb=1:10) for all inputs and one vector for all delays. Then only such models are computed that have the same orders and delays from all inputs.

Estimation Methods

There are two methods to estimate the coefficients a and b in the ARX model structure:

Least Squares: Minimizes the sum of squares of the right-hand side minus the left-hand side of the expression above, with respect to a and b. This is obtained by selecting ARX as the Method.

Instrumental Variables: Determines a and b so that the error between the right- and left- hand sides becomes uncorrelated with certain linear combinations of the inputs. This is obtained by selecting IV in the Method box.

The methods are described in more detail in the "Command Reference" chapter under arx and iv4.

Multi-Output Models

For a multi-output ARX structure with ny outputs and nu inputs, the difference equation above is still valid. The only change is that the coefficients a are ny-by-ny matrices and the coefficients b are ny-by-nu matrices.

The orders [NA NB NK] define the model structure as follows:

NA: an ny-by-ny matrix whose i-j entry is the order of the polynomial (in the delay operator) that relates the j-th output to the i-th output

NB: an ny-by-nu matrix whose i-j entry is the order of the polynomial that relates the j-th input to the i-th output

NK: an ny-by-nu matrix whose i-j entry is the delay from the j-th input to the i-th output

The Order Editor dialog box allows the choices

• NA = na*ones(ny,ny)
  NB = nb*ones(ny,nu)
  NK = nk*ones(ny,nu)
  

where na, nb, and nk are chosen by the pop-up menus.

For tailor-made order choices, construct a matrix [NA NB NK] in the MATLAB command window and enter the name of this matrix in the Order edit box in the Parametric Models window.

Note that the possibility to estimate many models simultaneously is not available for multi-output ARX models.

See Defining Model Structures for more information on multi-output ARX models.

Estimation of Parametric Models

ARMAX, Output-Error and Box-Jenkins Models