arx (System Identification Toolbox)

Estimate the parameters of an ARX or AR model.

Syntax

m = arx(data,orders)
m = arx(data,'na',na,'nb',nb,'nk',nk)
m= arx(data,orders,'Property1',Value1,...,'PropertyN',ValueN)

Description

The parameters of the ARX model structure

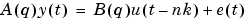
are estimated using the least-squares method.

data is an iddata object that contains the output-input data. orders is given as

```
orders = [na nb nk]
```

defining the orders and delay of the ARX model. Specifically,

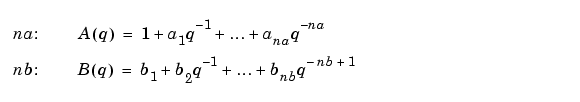
See Polynomial Representation of Transfer Functions in the "Tutorial" for more information. The model orders can also be defined by explicit pairs (...,'na',na,'nb',nb,'nk',nk,...).

m is returned as the least-squares estimates of the parameters. For single-output data this is an idpoly object, otherwise an idarx object.

For a time series, data contains no input channels and orders = na. Then an AR model of order na for y is computed.

Models with several inputs

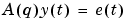
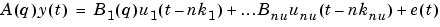
are handled by allowing nb and nk to be row vectors defining the orders and delays associated with each input.

Models with several inputs and several outputs are handled by allowing na, nb, and nk to contain one row for each output number. See Multivariable ARX Models: The idarx Model in the "Tutorial" for exact definitions.

The algorithm and model structure are affected by the property name/property value list in the input argument.

Useful options are reached by the properties 'Focus', 'InputDelay', and 'MaxSize'.

See Algorithm Properties for details of these properties and possible values

When the true noise term 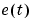in the ARX model structure is not white noise and na is nonzero, the estimate does not give a correct model. It is then better to use armax, bj, iv4, or oe.

Examples

Here is an example that generates data and estimates an ARX model.

A = [1  -1.5  0.7]; B = [0 1 0.5];
m0 = idpoly(A,B);
u = iddata([],idinput(300,'rbs'));
e = iddata([],randn(300,1));
y = sim(m0, [u e]);
z = [y,u];
m = arx(z,[2 2 1]);

Algorithm

The least squares estimation problem is an overdetermined set of linear equations that is solved using QR-factorization.

The regression matrix is formed so that only measured quantities are used (no fill-out with zeros). When the regression matrix is larger than MaxSize, the QR-factorization is performed in a for-loop.

armax arxdata