System Identification Toolbox

iv4

Estimate the parameters of an ARX model using an approximately optimal four-stage instrumental variable (IV) procedure.

Syntax

• m = iv4(data,orders)
  m = iv4(data,'na',na,'nb',nb,'nk',nk)
  m= iv4(data,orders,'Property1',Value1,...,'PropertyN',ValueN)
  

Description

This routine is an alternative to arx and the use of the arguments are entirely analogous to the arx function. The main difference is that the procedure is not sensitive to the color of the noise term 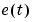in the model equation.

For an interpretation of the loss function (innovations covariance matrix), consult Interpretation of the Loss Function in the "Tutorial" chapter.

Examples

Here is an example of a two-input, one-output system with different delays on the inputs 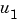and .

• z = iddata(y, [u1 u2]);
  nb = [2 2];
  nk = [0 2];
  m= iv4(z,[2 nb nk]);
  

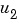Algorithm

The first stage uses the arx function. The resulting model generates the instruments for a second-stage IV estimate. The residuals obtained from this model are modeled as a high-order AR model. At the fourth stage, the input-output data are filtered through this AR model and then subjected to the IV function with the same instrument-filters as in the second stage.

For the multi-output case, optimal instruments are obtained only if the noise sources at the different outputs have the same color. The estimates obtained with the routine are reasonably accurate though even in other cases.

See Also

arx, oe

References

Ljung (1999), equations (15.21)-(15.26).

ivx

LTI Commands