rpem (System Identification Toolbox)

Estimate recursively the parameters of a general multi-input single-output linear model.

Syntax

thm = rpem(z,nn,adm,adg)
[thm,yhat,P,phi,psi] = rpem(z,nn,adm,adg,th0,P0,phi0,psi0)

Description

The parameters of the general linear model structure

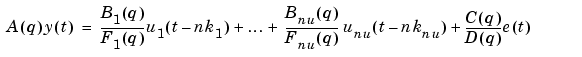
are estimated using a recursive prediction error method.

The input-output data are contained in z, which is either an iddata object or a matrix z = [y u] where y and u are column vectors. (In the multi-input case u contains one column for each input). nn is given as

```
nn = [na nb nc nd nf nk]
```

where na, nb, nc, nd, and nf are the orders of the model, and nk is the delay. For multi-input systems nb, nf, and nk are row vectors giving the orders and delays of each input. See Polynomial Representation of Transfer Functions in the "Tutorial" for an exact definition of the orders.

The estimated parameters are returned in the matrix thm. The k-th row of thm contains the parameters associated with time k, i.e., they are based on the data in the rows up to and including row k in z. Each row of thm contains the estimated parameters in the following order.

thm(k,:) = [a1,a2,...,ana,b1,...,bnb,...
  c1,...,cnc,d1,...,dnd,f1,...,fnf]

For multi-input systems the B part in the above expression is repeated for each input before the C part begins, and also the F part is repeated for each input. This is the same ordering as in m.par.

yhat is the predicted value of the output, according to the current model, i.e., row k of yhat contains the predicted value of y(k) based on all past data.

The actual algorithm is selected with the two arguments adg and adm. These are described under rarx.

The input argument th0 contains the initial value of the parameters;, a row vector, consistent with the rows of thm. (See above.) The default value of th0 is all zeros.

The arguments P0 and P are the initial and final values, respectively, of the scaled covariance matrix of the parameters. See rarx. The default value of P0 is 10⁴ times the unit matrix. The arguments phi0, psi0, phi, and psi contain initial and final values of the data vector and the gradient vector, respectively. The sizes of these depend in a rather complicated way on the chosen model orders. The normal choice of phi0 and psi0 is to use the outputs from a previous call to rpem with the same model orders. (This call could be a dummy call with default input arguments.) The default values of phi0 and psi0 are all zeros.

Note that the function requires that the delay nk is larger than 0. If you want nk=0 , shift the input sequence appropriately and use nk=1.

Algorithm

The general recursive prediction error algorithm (11.44) of Ljung (1999) is implemented. See also Recursive Parameter Estimation in the "Tutorial".

For the special cases of ARX/AR models, and of single-input ARMAX/ARMA, Box-Jenkins, and Output-Error models, it is more efficient to use rarx,
rarmax, rbj, and roe.

roe rplr