rarx (System Identification Toolbox)

Estimate recursively the parameters of an ARX or AR model.

Syntax

thm = rarx(z,nn,adm,adg)
[thm,yhat,P,phi] = rarx(z,nn,adm,adg,th0,P0,phi0)

Description

The parameters of the ARX model structure

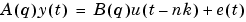
are estimated using different variants of the recursive least-squares method.

The input-output data are contained in z, which is either an iddata object or a matrix z = [y u] where y and u are column vectors. nn is given as

```
nn = [na nb nk]
```

where na and nb are the orders of the ARX model, and nk is the delay. Specifically,

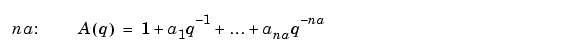
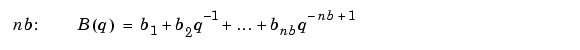
See equation (Equation 3-13) in the "Tutorial" for more information.

If z is a time series y and nn = na, rarx estimates the parameters of an AR model for y.

Models with several inputs

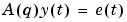
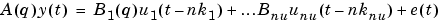
are handled by allowing u to contain each input as a column vector,

```
u = [u1 ...  unu]
```

and by allowing nb and nk to be row vectors defining the orders and delays associated with each input.

Only single-output models are handled by rarx.

The estimated parameters are returned in the matrix thm. The k-th row of thm contains the parameters associated with time k, i.e., they are based on the data in the rows up to and including row k in z. Each row of thm contains the estimated parameters in the following order.

```
thm(k,:) = [a1,a2,...,ana,b1,...,bnb]
```

In the case of a multi-input model, all the b parameters associated with input number 1 are given first, and then all the b parameters associated with input number 2, and so on.

yhat is the predicted value of the output, according to the current model, i.e., row k of yhat contains the predicted value of y(k) based on all past data.

The actual algorithm is selected with the two arguments adg and adm. These are described in Recursive Parameter Estimation in the "Tutorial" chapter. The options are as follows.

With adm ='ff' and adg = lam the forgetting factor algorithm (Equation 3-60abd)+(Equation 3-62) is obtained with forgetting factor 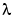= lam. This is what is often referred to as Recursive Least Squares, RLS. In this case the matrix P (see below) has the following interpretation: /2 * P is approximately equal to the covariance matrix of the estimated parameters. Here is the variance of the innovations (the true prediction errors e(t) in (Equation 3-57)

With adm ='ug' and adg = gam, the unnormalized gradient algorithm (Equation 3-60abc) + (Equation 3-63) is obtained with gain gamma= gam. This algorithm is commonly known as normalized Least Mean Squares, LMS.

Similarly, adm ='ng' and adg = gam give the normalized gradient or Normalized Least Mean Squares, NLMS algorithm (Equation 3-60abc) + (Equation 3-64). In these cases, P is not defined or applicable.

With adm ='kf' and adg = R1 the Kalman Filter Based algorithm (Equation 3-60) is obtained with R₂=1 and R₁ = R1. If the variance of the innovations e(t) is not unity but 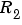; then 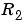* P is the covariance matrix of the parameter estimates, while 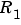=R1 /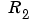 is the covariance matrix of the parameter changes in (Equation 3-58).

The input argument th0 contains the initial value of the parameters; a row vector, consistent with the rows of thm. (See above.) The default value of th0 is all zeros.

The arguments P0 and P are the initial and final values, respectively, of the scaled covariance matrix of the parameters. The default value of P0 is 10⁴ times the identity matrix.

The arguments phi0 and phi contain initial and final values, respectively, of the data vector.

Then, if

```
z = [y(1),u(1); ...  ;y(N),u(N)]
```

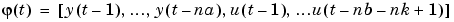
you have phi0 = and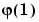 phi =. The default value of 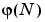phi0 is all zeros. For online use of rarx, use phi0, th0, and P0 as the previous outputs phi, thm (last row), and P.

Note that the function requires that the delay nk be larger than 0. If you want nk=0, shift the input sequence appropriately and use nk=1. See nkshift.

Examples

Adaptive noise canceling: The signal y contains a component that has its origin in a known signal r. Remove this component by estimating, recursively, the system that relates r to y using a sixth order FIR model together with the NLMS algorithm.

z = [y r];
[thm,noise] = rarx(z,[0 6 1],'ng',0.1);
% noise is the adaptive estimate of the noise
% component of y
plot(y-noise)

If the above application is a true online one, so that you want to plot the best estimate of the signal y - noise at the same time as the data y and u become available, proceed as follows.

phi = zeros(6,1); P=1000*eye(6);
th = zeros(1,6); axis([0 100 -2 2]);
plot(0,0,'*'), hold on
% The loop:
while ~abort
[y,r,abort] = readAD(time);
[th,ns,P,phi] = rarx([y r],'ff',0.98,th,P,phi);
plot(time,y-ns,'*')
time = time +Dt
end

This example uses a forgetting factor algorithm with a forgetting factor of 0.98. readAD represents an M-file that reads the value of an A/D converter at the indicated time instant.

rarmax rbj