idarx (System Identification Toolbox)

Construct idarx model from ARX polynomials.

Syntax

m = idarx(A,B,Ts)
m = idarx(A,B,Ts,'Property1',Value1,...,,'PropertyN',ValueN)

Description

idarx creates an object containing parameters that describe the general multi-input, multi-output model structure of ARX type.

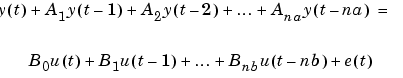
Here 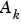and 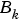are matrices of dimensions ny-by-ny and ny-by-nu, respectively (ny is the number of outputs, i.e., the dimension of the vector 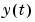and nu is the number of inputs). See Multivariable ARX Models: The idarx Model in the "Tutorial" chapter.

The arguments A and B are 3-D arrays that contain the A matrices and the B matrices of the model in the following way.

A is an ny-by-ny-by-(na+1) array such that

```
A(:,:,k+1) = Ak
A(:,:,1) = eye(ny)
```

Similairly B is an ny-by-nu-by-(nb+1) array with

```
B(:,:,k+1) = Bk
```

Note that A always starts with the identity matrix, and that delays in the model are defined by setting the corresponding leading entries in B to zero. For a multivariate time series take B = [].

The optional property NoiseVariance sets the covariance matrix of the driving noise source 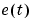in the model above. The default value is the identity matrix.

The argument Ts is the sampling interval.

The use of idarx is twofold. You can use it to create models that are simulated (using sim) or analyzed (using bode, pzmap, etc.). You can also use it to define initial value models that are further adjusted to data (using arx). The free parameters in the structure are consistent with the structure of A and B, i.e., leading zeros in the rows of B are regarded as fixed delays, and trailing zeros in A and B are regarded as a definition of lower order polynomials. These zeros are fixed, while all other parameters are free.

For a model with one output, ARX models can be descried both as idarx and idpoly models. The internal representation is however different.

idarx Properties

A, B: The A and B polynomials as 3-D arrays, described above
dA, dB: The standard deviations of A and B. Same format as A and B. Cannot be set.
na, nb, nk: The orders and delays of the model. na is a ny-by-ny matrix whose i-j entry is the order of the polynomial corresponding to the i-j entry of A. Similarly nb is an ny-by-nu matrix with the orders of the B. nk is also an ny-by-nu matrix, whose i-j entry is the delay from input j to output i, that is, the number of leading zeros in the i-j entry of B.

In addition to these properties, idarx objects also have all the properties of the idmodel object. See idmodel, Algorithm Properties, and EstimationInfo.

Note that all properties can be set and retrieved either by set/get or by subscripts. Autofill applies to all properties and values, and these are case insensitive.

For a complete list of property values, use get(m). To see possible value assignments, use set(m). See also idprops idarx.

Examples

Simulate a second order ARX model with one input and two outputs, and then estimate a model using the simulated data.

A = zeros(2,2,3);
B = zeros(2,1,3)
A(:,:,1) =eye(2);
A(:,:,2) = [-1.5 0.1;-0.2 1.5];
A(:,:,3) = [0.7 -0.3;0.1 0.7];
B(:,:,2) = [1;-1];
B(:,:,3) = [0.5;1.2];
m0 = idarx(A,B,1);
u = iddata([],idinput(300));
e = iddata([],randn(300,2));
y = sim(m0,[u e]);
m = arx([y u],[[2 2;2 2],[2;2],[1;1]]);

See Also

arx, arxdata, idmodel, idpoly

getexp iddata