Wavelet Toolbox

cwt

Continuous 1-D wavelet coefficients

Syntax

• COEFS = cwt(S,SCALES,'wname')
  COEFS = cwt(S,SCALES,'wname','plot')
  COEFS = cwt(S,SCALES,'wname',PLOTMODE)
  COEFS = cwt(S,SCALES,'wname',PLOTMODE,XLIM)
  

Description

cwt is a one-dimensional wavelet analysis function.

COEFS = cwt(S,SCALES,'wname') computes the continuous wavelet coefficients of the vector S at real, positive SCALES, using the wavelet whose name is 'wname' (see waveinfo for more information).

The signal S is real, the wavelet can be real or complex.

COEFS = cwt(S,SCALES,'wname','plot') computes and, in addition, plots the continuous wavelet transform coefficients.

COEFS = cwt(S,SCALES,'wname',PLOTMODE) computes and plots the continuous wavelet transform coefficients.

Coefficients are colored using PLOTMODE. Valid values for the string PLOTMODE are listed in the table below.

PLOTMODE	Description
'lvl'	Coloration made scale-by-scale
'glb'	Coloration made considering all scales
'abslvl' or 'lvlabs'	Coloration made scale-by-scale using the absolute values of the coefficients
'absglb' or 'glbabs'	Coloration made considering all scales using the absolute values of the coefficients

COEFS = cwt(...,'plot') is equivalent to COEFS = cwt(...,'absglb')

Note    You can get 3-D plots (surfaces) using the same keywords listed above for the PLOTMODE parameter, preceded by '3D'. For example: COEFS = cwt(...,'3Dplot')or COEFS = cwt(...,'3Dlvl') ...

COEFS = cwt(S,SCALES,'wname',PLOTMODE,XLIM) computes and plots the continuous wavelet transform coefficients.

Coefficients are colored using PLOTMODE and XLIM.

XLIM = [x1 x2] with 1 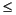x1 < x2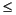 length(S)

Let s be the signal and 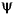the wavelet. The wavelet coefficient of s at scale a and position b is defined by

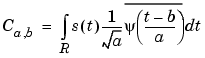
Since s(t) is a discrete signal, we use a piecewise constant interpolation of the s(k) values, k = 1 to length(s).

For each given scale a within the vector SCALES, the wavelet coefficients C_a,b are computed for b = 1 to ls = length(s), and are stored in COEFS(i,:) if a = SCALES(i).

Output argument COEFS is a la-by-ls matrix where la is the length of SCALES. COEFS is a real or complex matrix depending on the wavelet type.

Examples of valid uses are

• t = linspace(-1,1,512);
  s = 1-abs(t);
  c = cwt(s,1:32,'cgau4');
  c = cwt(s,[64 32 16:-2:2],'morl');
  c = cwt(s,[3 18 12.9 7 1.5],'db2');
  c = cwt(s,1:64,'sym4','abslvl',[100 400]);
  

Examples

This example demonstrates the difference between discrete and continuous wavelet transforms.

• % Load a fractal signal. 
  load vonkoch 
  vonkoch=vonkoch(1:510); 
  lv = length(vonkoch);
  
  subplot(311), plot(vonkoch);title('Analyzed signal.'); 
  set(gca,'Xlim',[0 510])
  % Perform discrete wavelet transform at level 5 by sym2. 
  % Levels 1 to 5 correspond to scales 2, 4, 8, 16 and 32. 
  [c,l] = wavedec(vonkoch,5,'sym2');
  
  % Expand discrete wavelet coefficients for plot. 
  % Levels 1 to 5 correspond to scales 2, 4, 8, 16 and 32. 
  cfd = zeros(5,lv); 
  for k = 1:5 
      d = detcoef(c,l,k); 
      d = d(ones(1,2^k),:); 
      cfd(k,:) = wkeep(d(:)',lv); 
  end 
  
  cfd = cfd(:); 
  I = find(abs(cfd)<sqrt(eps)); 
  cfd(I)=zeros(size(I)); 
  cfd = reshape(cfd,5,lv);
  
  % Plot discrete coefficients. 
  subplot(312), colormap(pink(64)); 
  img = image(flipud(wcodemat(cfd,64,'row'))); 
  set(get(img,'parent'),'YtickLabel',[]); 
  title('Discrete Transform, absolute coefficients.') 
  ylabel('level')
  
  % Perform continuous wavelet transform by sym2 at all integer 
  % scales from 1 to 32. 
  subplot(313)
  ccfs = cwt(vonkoch,1:32,'sym2','plot'); 
  title('Continuous Transform, absolute coefficients.') 
  colormap(pink(64)); 
  ylabel('Scale')
  
  % Editing some graphical properties,
  % the following figure is generated.
  
  
  

Algorithm

if s(t) = s(k), for then

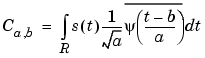
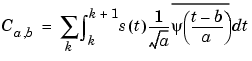
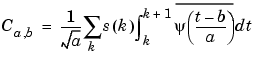
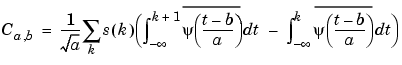
So at any scale a, the wavelet coefficients C_a,b for b = 1 to length(s) can be obtained by convolving the signal s and a dilated and translated version of the

integrals of the form

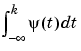(given by intwave), and taking the finite difference using diff.

See Also
wavedec, wavefun, waveinfo, wcodemat

coifwavf

dbaux