Wavelet Toolbox

dbaux

Daubechies wavelet filter computation

Syntax

• W = dbaux(N,SUMW)
  W = dbaux(N)
  

Description

W = dbaux(N,SUMW) is the order N Daubechies scaling filter such that sum(W) = SUMW. Possible values for N are 1, 2, 3, ...

Note    Instability may occur when N is too large.

W = dbaux(N) is equivalent to W = dbaux(N,1)

W = dbaux(N,0) is equivalent to W = dbaux(N,1)

Examples

• % P the "Lagrange à trous" filter for N=2 is explicit 
  % and given by: 
  P = [ -1/16 0 9/16 1 9/16 0 -1/16]
  
  P =
     -0.0625        0  0.5625  1.0000  0.5625        0 -0.0625
  
  % The db2 Daubechies scaling filter w, is a 
  % solution of the equation: P = conv(wrev(w),w) * 2.
  %
  % This filter P is symmetric, easy to generate, and w is 
  % a minimum phase solution of the previous equation, 
  % based on the roots of P. 
  rP = roots(P);
  
  % Retaining only the root inside the unit circle (here it
  % is the sixth value of rP), and two roots located at -1, 
  % we obtain the Daubechies wavelet of order 2:
  ww = poly([rP(6) -1 -1]);    % filter construction
  ww = ww / sum(ww)            % normalize sum
  
  ww =
      0.3415  0.5915  0.1585 -0.0915
  
  % Check that ww is correct and equal to 
  % the db2 Daubechies scaling filter w. 
  w = dbaux(2)
  
  w =
      0.3415  0.5915  0.1585 -0.0915
  

Algorithm

The algorithm used is based on a result obtained by Shensa (see "References"), showing a correspondence between the "Lagrange à trous" filters and the convolutional squares of the Daubechies wavelet filters.

The computation of the order N Daubechies scaling filter w proceeds in two steps: compute a "Lagrange à trous" filter P, and extract a square root. More precisely:

• P the associated "Lagrange à trous" filter is a symmetric filter of length
  4N-1. P is defined by

  P = [a(N) 0 a(N-1) 0 ... 0 a(1) 1 a(1) 0 a(2) 0 ... 0 a(N)]

  where

• Then, if w denotes dbN Daubechies scaling filter of sum , w is a square root of P:

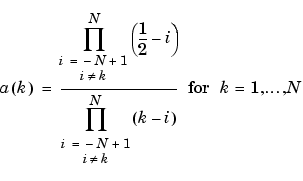
•                    P = conv(wrev(w),w) where w is a filter of length 2N.

  The corresponding polynomial has N zeros located at -1 and N-1 zeros less than 1 in modulus.

Note that other methods can be used; see various solutions of the spectral factorization problem in Strang-Nguyen (p. 157).

Limitations

The computation of the dbN Daubechies scaling filter requires the extraction of the roots of a polynomial of order 4N. Instability may occur when N is too large.

See Also
dbwavf, wfilters

References

Daubechies, I. (1992), Ten lectures on wavelets, CBMS-NSF conference series in applied mathematics, SIAM Ed.

Shensa, M.J. (1992), "The discrete wavelet transform: wedding the a trous and Mallat Algorithms," IEEE Trans. on Signal Processing, vol. 40, 10,
pp. 2464-2482.

Strang, G.; T. Nguyen (1996), Wavelets and Filter Banks, Wellesley-Cambridge Press.

cwt

dbwavf