prony (Signal Processing Toolbox)

Prony's method for time domain IIR filter design

Syntax

```
[b,a] = prony(h,n,m)
```

Description

Prony's method is an algorithm for finding an IIR filter with a prescribed time domain impulse response. It has applications in filter design, exponential signal modeling, and system identification (parametric modeling).

[b,a] = prony(h,n,m) finds a filter with numerator order n, denominator order m, and the time domain impulse response in h. If the length of h is less than the largest order (n or m), h is padded with zeros. prony returns the filter coefficients in row vectors b and a, of length n + 1 and m + 1, respectively. The filter coefficients are in descending powers of z.

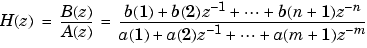
Examples

Recover the coefficients of a Butterworth filter from its impulse response:

[b,a] = butter(4,0.2)
b = 
    0.0048    0.0193    0.0289    0.0193    0.0048
a =
    1.0000    -2.3695    2.3140    -1.0547    0.1874
h = filter(b,a,[1 zeros(1,25)]);
[bb,aa] = prony(h,4,4)
bb = 
    0.0048    0.0193    0.0289    0.0193    0.0048
ab =
    1.0000    -2.3695    2.3140    -1.0547    0.1874

Algorithm

prony implements the method described in reference [1]. This method uses a variation of the covariance method of AR modeling to find the denominator coefficients a and then finds the numerator coefficients b for which the impulse response of the output filter matches exactly the first n + 1 samples of x. The filter is not necessarily stable, but potentially can recover the coefficients exactly if the data sequence is truly an autoregressive moving average (ARMA) process of the correct order.

See Also

butter, cheby1, cheby2, ellip, invfreqz, levinson, lpc, stmcb

References

[1] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, 1987, pp. 226-228.

polystab psdplot