Signal Processing Toolbox

levinson

Compute the Levinson-Durbin recursion

Syntax

• a = levinson(r,p)
  

Description

The Levinson-Durbin recursion is an algorithm for finding an all-pole IIR filter with a prescribed deterministic autocorrelation sequence. It has applications in filter design, coding, and spectral estimation. The filter that levinson produces is minimum phase.

a = levinson(r,p) finds the coefficients of an pth-order autoregressive linear process which has r as its autocorrelation sequence. r is a real or complex deterministic autocorrelation sequence (a vector), and p is the order of denominator polynomial A(z); that is, a = [1 a(2) ... a(p+1)]. The filter coefficients are ordered in descending powers of z.

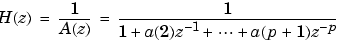
Algorithm

levinson solves the symmetric Toeplitz system of linear equations

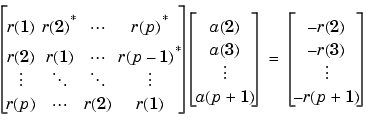
where r = [r(1)  ... r(p+1)] is the input autocorrelation vector, and r(i)^* denotes the complex conjugate of r(i). The algorithm requires O(p²) flops and is thus much more efficient than the MATLAB \ command for large p. However, the levinson function uses \ for low orders to provide the fastest possible execution.

See Also

lpc, prony, rlevinson, schurrc, stmcb

References

[1] Ljung, L., System Identification: Theory for the User, Prentice-Hall, 1987, pp. 278-280.

latcfilt

lp2bp