Optimization Toolbox

Nonlinear Minimization with Bound Constraints and Banded Preconditioner

The goal in this problem is to minimize the nonlinear function

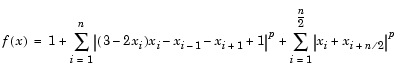
such that 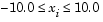, where n is 800 (n should be a multiple of 4), 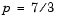, and .

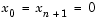Step 1: Write an M-file tbroyfg.m that computes the objective function and the gradient of the objective

The M-file function tbroyfg.m computes the function value and gradient. This file is long and is not included here. You can see the code for this function using the command

• type tbroyfg
  

The sparsity pattern of the Hessian matrix has been predetermined and stored in the file tbroyhstr.mat. The sparsity structure for the Hessian of this problem is banded, as you can see in the followint spy plot.

• load tbroyhstr
  spy(Hstr)
  

In this plot, the center stripe is itself a five-banded matrix. The following plot shows the matrix more clearly:

• spy(Hstr(1:20,1:20))
  

Use optimset to set the HessPattern parameter to Hstr. When a problem as large as this has obvious sparsity structure, not setting the HessPattern parameter requires a huge amount of unnecessary memory and computation. This is because fmincon attempts to use finite differencing on a full Hessian matrix of 640,000 nonzero entries.

You must also set the GradObj parameter to 'on' using optimset, since the gradient is computed in tbroyfg.m. Then execute fmincon as shown in Step 2.

Step 2: Call a nonlinear minimization routine with a starting point xstart.

• fun = @tbroyfg;
  load tbroyhstr          % Get Hstr, structure of the Hessian
  n = 800;
  xstart = -ones(n,1); xstart(2:2:n) = 1;
  lb = -10*ones(n,1); ub = -lb;
  options = optimset('GradObj','on','HessPattern',Hstr); 
  [x,fval,exitflag,output] = ... 
     fmincon(fun,xstart,[],[],[],[],lb,ub,[],options);
  

After eight iterations, the exitflag, fval, and output values are

• exitflag =
       1
  fval =
    270.4790
  output = 
       iterations: 8
        funcCount: 8
     cgiterations: 18
    firstorderopt: 0.0163
        algorithm: 'large-scale: trust-region reflective Newton'
  

For bound constrained problems, the first-order optimality is the infinity norm of v.*g, where v is defined as in Box Constraints, and g is the gradient.

Because of the five-banded center stripe, you can improve the solution by using a five-banded preconditioner instead of the default diagonal preconditioner. Using the optimset function, reset the PrecondBandWidth parameter to 2 and solve the problem again. (The bandwidth is the number of upper (or lower) diagonals, not counting the main diagonal.)

• fun = @tbroyfg;
  load tbroyhstr          % Get Hstr, structure of the Hessian
  n = 800;
  xstart = -ones(n,1); xstart(2:2:n,1) = 1;
  lb = -10*ones(n,1); ub = -lb;
  options = optimset('GradObj','on','HessPattern',Hstr, ...
                     'PrecondBandWidth',2); 
  [x,fval,exitflag,output] = ...
     fmincon(fun,xstart,[],[],[],[],lb,ub,[],options); 
  

The number of iterations actually goes up by two; however the total number of CG iterations drops from 18 to 15. The first-order optimality measure is reduced by a factor of 1e-3:

• exitflag =
       1
  fval =
    2.7048e+002
  output = 
       iterations: 10
        funcCount: 10
     cgiterations: 15
    firstorderopt: 7.5339e-005
        algorithm: 'large-scale: trust-region reflective Newton'
  

Nonlinear Minimization with Gradient and Hessian Sparsity Pattern

Nonlinear Minimization with Equality Constraints