Optimization Toolbox

quadprog

Solve the quadratic programming problem

where H, A, and Aeq are matrices, and f, b, beq, lb, ub, and x are vectors.

Syntax

• x = quadprog(H,f,A,b)
  x = quadprog(H,f,A,b,Aeq,beq)
  x = quadprog(H,f,A,b,Aeq,beq,lb,ub)
  x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)
  x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
  x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...)
  [x,fval] = quadprog(...)
  [x,fval,exitflag] = quadprog(...)
  [x,fval,exitflag,output] = quadprog(...)
  [x,fval,exitflag,output,lambda] = quadprog(...)
  

Description

x = quadprog(H,f,A,b) returns a vector x that minimizes 1/2*x'*H*x + f'*x subject to A*x <= b.

x = quadprog(H,f,A,b,Aeq,beq) solves the problem above while additionally satisfying the equality constraints Aeq*x = beq.

x = quadprog(H,f,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that the solution is in the range lb <= x <= ub.

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0) sets the starting point to x0.

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options,p1,p2,...) passes parameters p1,p2,... to the Hessian multiply function, if it exists, specified using the HessMult parameter in the options structure.

[x,fval] = quadprog(...) returns the value of the objective function at x: fval = 0.5*x'*H*x + f'*x.

[x,fval,exitflag] = quadprog(...) returns a value exitflag that describes the exit condition of quadprog.

[x,fval,exitflag,output] = quadprog(...) returns a structure output that contains information about the optimization.

[x,fval,exitflag,output,lambda] = quadprog(...) returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to quadprog. Options provides function-specific details for the options parameters.

Output Arguments

Function Arguments contains general descriptions of arguments returned by quadprog. This section provides function-specific details for exitflag, lambda, and output:

exitflag	Describes the exit condition:
	> 0	The function converged to a solution x.
	0	The maximum number of function evaluations or iterations was exceeded.
	< 0	The function did not converge to a solution.
lambda	Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields are:
	lower	For the lower bounds lb
	upper	For the upper bounds ub
	ineqlin	For the linear inequalities
	eqlin	For the linear equalities
output	Structure containing information about the optimization. The fields are:
	iterations	Number of iterations taken
	algorithm	Algorithm used
	cgiterations	Number of PCG iterations (large-scale algorithm only)
	firstorderopt	Measure of first-order optimality (large-scale algorithm only) For large-scale bound constrained problems, the first-order optimality is the infinity norm of v.*g, where v is defined as in Box Constraints, and g is the gradient. For large scale problems with linear equalities only, the first-order optimality is the 2-norm of the scaled residual (z = M\r) of the Reduced Preconditioned Conjugate Gradient calculation. See Algorithm in "Preconditioned Conjugate Gradients," and also Linearly Constrained Problems.

Options

Optimization parameter options. Use optimset to set or change the values of these parameters. Some parameters apply to all algorithms, some are only relevant when using the large-scale algorithm, and others are only relevant when using the medium-scale algorithm. See Optimization Parameters for detailed nformation.

The parameter to set an algorithm preference:

LargeScale

Use large-scale algorithm if possible when set to 'on'. Use medium-scale algorithm when set to 'off'. 'on' is only a preference. If the problem has only upper and lower bounds, i.e., no linear inequalities or equalities are specified, the default algorithm is the large-scale method. Or, if the problem given to quadprog has only linear equalities, i.e., no upper and lower bounds or linear inequalities are specified, and the number of equalities is no greater than the length of x, the default algorithm is the large-scale method. Otherwise the medium-scale algorithm is used.

Medium-Scale and Large-Scale Algorithms.   These parameters are used by both the medium-scale and large-scale algorithms:

Diagnostics	Print diagnostic information about the function to be minimized.
Display	Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output.
MaxIter	Maximum number of iterations allowed.

Large-Scale Algorithm Only.   These parameters are used only by the large-scale algorithm:

HessMult	Function handle for Hessian multiply function. For large-scale structured problems, this function computes the Hessian matrix product H*Y without actually forming H. The function is of the form W = hmfun(Hinfo,Y,p1,p2,...) where Hinfo and the additional parameters p1,p2,... contain the matrices used to compute H*Y. Hinfo is the same as the first argument of quadprog and p1,p2,... are the same additional parameters that are passed to quadprog. quadprog(Hinfo,...,options,... p1,p2,...) Y is a matrix that has the same number of rows as there are dimensions in the problem. W = H*Y although H is not formed explicitly. quadprog uses Hinfo to compute the preconditioner. See Quadratic Minimization with a Dense but Structured Hessian for an example.
MaxPCGIter	Maximum number of PCG (preconditioned conjugate gradient) iterations (see the Algorithm section below).
PrecondBandWidth	Upper bandwidth of preconditioner for PCG. By default, diagonal preconditioning is used (upper bandwidth of 0). For some problems, increasing the bandwidth reduces the number of PCG iterations.
TolFun	Termination tolerance on the function value. TolFun is used as the exit criteria for problems with simple lower and upper bounds (lb, ub).
TolPCG	Termination tolerance on the PCG iteration. TolPCG is used as the exit criteria for problems with only equality constraints (Aeq, beq).
TolX	Termination tolerance on x.
TypicalX	Typical x values.

Examples

Find values of x that minimize

subject to

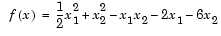
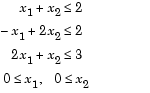
First, note that this function can be written in matrix notation as

where

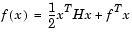
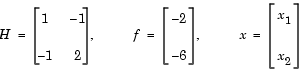
Enter these coefficient matrices.

• H = [1 -1; -1 2] 
  f = [-2; -6]
  A = [1 1; -1 2; 2 1]
  b = [2; 2; 3]
  lb = zeros(2,1)
  

Next, invoke a quadratic programming routine.

• [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)
  

This generates the solution

• x = 
       0.6667
       1.3333
  fval =
      -8.2222
  exitflag =
       1
  output = 
         iterations: 3
          algorithm: 'medium-scale: active-set'
      firstorderopt: []
       cgiterations: []
  lambda.ineqlin
  ans =
      3.1111
      0.4444
           0
  lambda.lower
  ans =
       0
       0
  

Nonzero elements of the vectors in the fields of lambda indicate active constraints at the solution. In this case, the first and second inequality constraints (in lambda.ineqlin) are active constraints (i.e., the solution is on their constraint boundaries). For this problem, all the lower bounds are inactive.

Notes

In general quadprog locates a local solution unless the problem is strictly convex.

Better numerical results are likely if you specify equalities explicitly using Aeq and beq, instead of implicitly using lb and ub.

If components of x have no upper (or lower) bounds, then quadprog prefers that the corresponding components of ub (or lb) be set to Inf (or -Inf for lb) as opposed to an arbitrary but very large positive (or negative in the case of lower bounds) number.

Large-Scale Optimization.   If you do not supply x0, or x0 is not strictly feasible, quadprog chooses a new strictly feasible (centered) starting point.

If an equality constrained problem is posed and quadprog detects negative curvature, then the optimization terminates because the constraints are not restrictive enough. In this case, exitflag is returned with the value -1, a message is displayed (unless the options Display parameter is 'off'), and the x returned is not a solution but a direction of negative curvature with respect to H.

For problems with simple lower and upper bounds (lb, ub), quadprog exits based on the value of TolFun. For problems with only equality constraints (Aeq, beq), the exit is based on TolPCG. Adjust TolFun and TolPCG to affect your results. TolX is used by both type of problems.

Algorithm

Large-Scale Optimization.   When the problem given to quadprog has only upper and lower bounds, i.e., no linear inequalities or equalities are specified, the default algorithm is the large-scale method. Or, if the problem given to quadprog has only linear equalities, i.e., no upper and lower bounds or linear inequalities are specified, the default algorithm is the large-scale method.

This method is a subspace trust-region method based on the interior-reflective Newton method described in [1]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG). See Trust-Region Methods for Nonlinear Minimization and Preconditioned Conjugate Gradients.

Medium-Scale Optimization.   quadprog uses an active set method, which is also a projection method, similar to that described in [2]. It finds an initial feasible solution by first solving a linear programming problem. This method is discussed in the Standard Algorithms chapter.

Diagnostics

Large-Scale Optimization.   The large-scale code does not allow equal upper and lower bounds. For example if lb(2) == ub(2) then quadprog gives the error

• Equal upper and lower bounds not permitted in this large-scale 
  method.
  Use equality constraints and the medium-scale method instead.
  

If you only have equality constraints you can still use the large-scale method. But if you have both equalities and bounds, you must use the medium-scale method.

Medium-Scale Optimization.   When the solution is infeasible, quadprog gives this warning

• Warning: The constraints are overly stringent;
       there is no feasible solution.
  

In this case, quadprog produces a result that minimizes the worst case constraint violation.

When the equality constraints are inconsistent, quadprog gives this warning

• Warning: The equality constraints are overly stringent;
       there is no feasible solution.
  

Unbounded solutions,which can occur when the Hessian H is negative semidefinite, may result in

• Warning: The solution is unbounded and at infinity;
       the constraints are not restrictive enough.
  

In this case, quadprog returns a value of x that satisfies the constraints.

Limitations

At this time the only levels of display, using the Display parameter in options, are 'off' and 'final'; iterative output using 'iter' is not available.

The solution to indefinite or negative definite problems is often unbounded (in this case, exitflag is returned with a negative value to show a minimum was not found); when a finite solution does exist, quadprog may only give local minima since the problem may be nonconvex.

Large-Scale Optimization.   The linear equalities cannot be dependent (i.e., Aeq must have full row rank). Note that this means that Aeq cannot have more rows than columns. If either of these cases occur, the medium-scale algorithm is called instead. See Table 2-4, Large-Scale Problem Coverage and Requirements,, for more information on what problem formulations are covered and what information must be provided.

References

[1]  Coleman, T.F. and Y. Li, "A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on some of the Variables," SIAM Journal on Optimization, Vol. 6, Number 4, pp. 1040-1058, 1996.

[2]  Gill, P. E. and W. Murray, and M.H. Wright, Practical Optimization, Academic Press, London, UK, 1981.

optimset