Function Reference

place

Pole placement design

Syntax

• K = place(A,B,p)
  [K,prec,message] = place(A,B,p)
  

Description

Given the single- or multi-input system

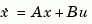
and a vector p of desired self-conjugate closed-loop pole locations, place computes a gain matrix K such that the state feedback 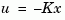places the closed-loop poles at the locations p. In other words, the eigenvalues of 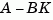match the entries of p (up to the ordering).

K = place(A,B,p) computes a feedback gain matrix K that achieves the desired closed-loop pole locations p, assuming all the inputs of the plant are control inputs. The length of p must match the row size of A. place works for multi-input systems and is based on the algorithm from [1]. This algorithm uses the extra degrees of freedom to find a solution that minimizes the sensitivity of the closed-loop poles to perturbations in 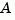or .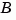

[K,prec,message] = place(A,B,p) also returns prec, an estimate of how closely the eigenvalues of 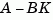match the specified locations p (prec measures the number of accurate decimal digits in the actual closed-loop poles). If some nonzero closed-loop pole is more than 10% off from the desired location, message contains a warning message.

You can also use place for estimator gain selection by transposing the A matrix and substituting C' for B.

• l = place(A',C',p).'
  

Example

Consider a state-space system (a,b,c,d) with two inputs, three outputs, and three states. You can compute the feedback gain matrix needed to place the closed-loop poles at p = [1.1 23 5.0] by

• p = [1 1.23 5.0];
  K = place(a,b,p)
  

Algorithm

place uses the algorithm of [1] which, for multi-input systems, optimizes the choice of eigenvectors for a robust solution. We recommend place rather than acker even for single-input systems.

In high-order problems, some choices of pole locations result in very large gains. The sensitivity problems attached with large gains suggest caution in the use of pole placement techniques. See [2] for results from numerical testing.

See Also
acker       Pole placement using Ackermann's formula

lqr         State-feedback LQ regulator design

rlocus      Root locus design

References

[1] Kautsky, J. and N.K. Nichols, "Robust Pole Assignment in Linear State Feedback," Int. J. Control, 41 (1985), pp. 1129-1155.

[2] Laub, A.J. and M. Wette, Algorithms and Software for Pole Assignment and Observers, UCRL-15646 Rev. 1, EE Dept., Univ. of Calif., Santa Barbara, CA, Sept. 1984.

parallel

pole