freqresp (Function Reference)

Compute frequency response over grid of frequencies

Syntax

```
H = freqresp(sys,w)
```

Description

H = freqresp(sys,w) computes the frequency response of the LTI model sys at the real frequency points specified by the vector w. The frequencies must be in radians/sec. For single LTI Models, freqresp(sys,w) returns a 3-D array H with the frequency as the last dimension (see "Arguments" below). For LTI arrays of size [Ny Nu S1 ... Sn], freqresp(sys,w) returns a [Ny-by-Nu-by-S1-by-...-by-Sn] length (w) array.

In continuous time, the response at a frequency 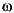is the transfer function value at 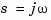. For state-space models, this value is given by

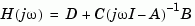
In discrete time, the real frequencies w(1),..., w(N) are mapped to points on the unit circle using the transformation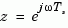

where 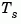is the sample time. The transfer function is then evaluated at the resulting 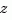values. The default 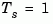is used for models with unspecified sample time.

Remark

If sys is an FRD model, freqresp(sys,w), w can only include frequencies in sys.frequency. Interpolation and extrapolation are not supported. To interpolate an FRD model, use interp.

Arguments

The output argument H is a 3-D array with dimensions

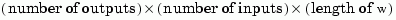
For SISO systems, H(1,1,k) gives the scalar response at the frequency w(k). For MIMO systems, the frequency response at w(k) is H(:,:,k), a matrix with as many rows as outputs and as many columns as inputs.

Example

Compute the frequency response of

at the frequencies . Type

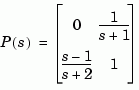
w = [1 10 100]
H = freqresp(P,w)
H(:,:,1) =
 
        0            0.5000- 0.5000i
  -0.2000+ 0.6000i   1.0000         
 
 
H(:,:,2) =
 
        0            0.0099- 0.0990i
   0.9423+ 0.2885i   1.0000         
 
 
H(:,:,3) =
 
        0            0.0001- 0.0100i
   0.9994+ 0.0300i   1.0000

The three displayed matrices are the values of 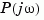for

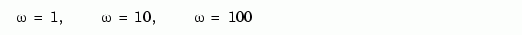
The third index in the 3-D array H is relative to the frequency vector w, so you can extract the frequency response at 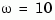rad/sec by

H(:,:,w==10)

ans =
        0            0.0099- 0.0990i
   0.9423+ 0.2885i   1.0000

Algorithm

For transfer functions or zero-pole-gain models, freqresp evaluates the numerator(s) and denominator(s) at the specified frequency points. For continuous-time state-space models 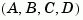, the frequency response is

For efficiency, 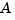is reduced to upper Hessenberg form and the linear equation 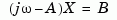is solved at each frequency point, taking advantage of the Hessenberg structure. The reduction to Hessenberg form provides a good compromise between efficiency and reliability. See [1] for more details on this technique.

Diagnostics

If the system has a pole on the axis (or unit circle in the discrete-time case) and w happens to contain this frequency point, the gain is infinite, 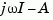is singular, and freqresp produces the following warning message.

Singularity in freq. response due to jw-axis or unit circle pole.

See Also
evalfr Response at single complex frequency

bode Bode plot

nyquist Nyquist plot

nichols Nichols plot

sigma Singular value plot

ltiview LTI system viewer

interp Interpolate FRD model between frequency points

References

[1] Laub, A.J., "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 407-408.

frdata gensig